相對論性最小作用量原理

Author:Peir-Ru Wang
\(\to\)English Version
\(\to\)Lecture Note-Principle of Least Action(2019)
\(\to\)Lecture Note-Principle of Least Action(2018)

Update 2024.12.03：新增-淺談希爾伯特變分
Update 2024.12.02：新增-邁向廣義相對論

  1. 淺談Particle與EM Field交互作用下的Action

    2. 以前我們學古典力學時，完整描述一個Particle只須寫下它的Lagrangian $$S=\int _a^b Ldt=\int _a^b T-U dt $$ $$=\int _a^b T dt +\int _a^b -U dt =S_P+S_{PF}$$ 其中，動能項\(T\)可視為Free particle的Action \(S_P\)，位能項\(U\)就是Particle和Field交互作用的Action \(S_{PF}\)。在電磁學我們學到Field也有帶有動量、能量，所以完整描述電磁運動會包含Field的Action \(S_F\) $$S=S_P+S_{PF}+S_F$$

  2. Free Particle Action的變分

    3. 在相對論性下，描述Free particle我們會利用4-displacement $$\eta =\eta ^\mu \hat{e} _\mu =(\tau ,\overrightarrow{0} )_{porper}=(t,\overrightarrow{\eta})$$ 來描述粒子的軌跡，其中\(\tau\) 是particle的proper time。這邊採用\(\eta ^\mu\) 與\(x^\mu\) 區分軌跡與時空（因應後續諾特定理討論，需嚴謹區分軌跡和時空，軌跡是物理量，時空是座標，是不同的概念）；描述粒子速度利用4-Velocity \(U=U^\mu \hat{e} _\mu =(\gamma c,\gamma \overrightarrow{v} )={d\eta ^\mu \over d\tau} \hat{e} _\mu\) ，其中\(\tau\) 是particle的proper time。更進一步說\(U^\mu =U^\mu (x^\nu )\)，速度\(U^\mu\) 會隨在時空的不同座標\(x^\nu\) 發生改變。在這邊的想法是，一個Free particle從時空中a跑到b，我們針對不同路徑\(\eta ^\mu\) 下的Action \(S_P\)去算極值，即對\(x^\mu\) 作變分
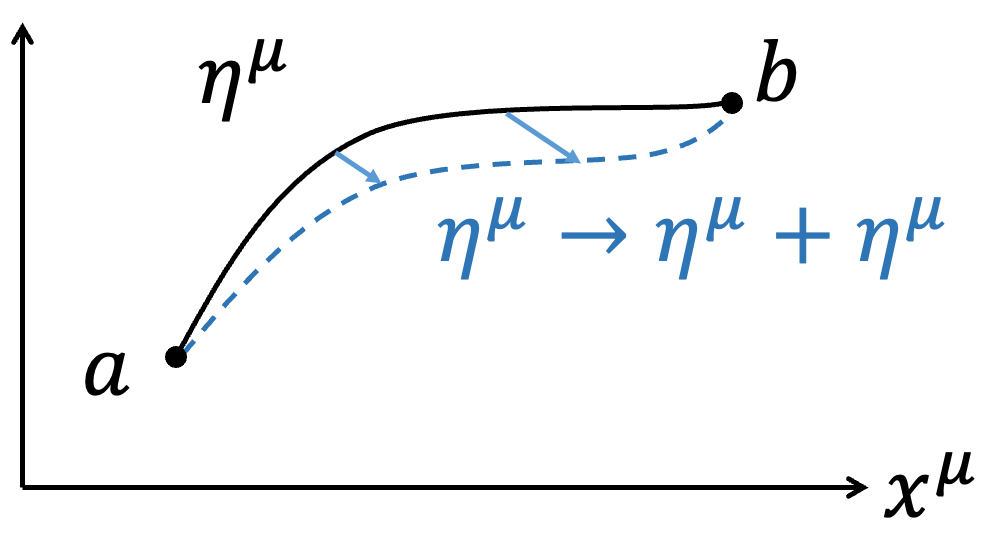    取代文字 $$\eta ^\mu \to \eta ^\mu +\delta \eta ^\mu $$ $$\delta \eta ^\mu (a)=\delta \eta ^\mu (b)=0$$ Free particle的Action \(S_P\)為 $$S_P=\int _a^b -mc^2 d\tau $$ 經過變分 $$\delta S_P=\delta \int _a^b -mc^2 d\tau =-mc^2 \int _a^b \delta d\tau $$ 看起來\(d\tau \)好像與\(\eta ^\mu \to \eta ^\mu +\delta \eta ^\mu\) 變分無關，不過回憶一件事情 $$∵c^2 d\tau ^2=d\eta ^\mu d\eta _\mu $$ $$∴cd\tau =\sqrt{d\eta ^\mu d\eta _\mu}$$ 所以 $$\delta S_P=-mc\int _a^b \delta \sqrt{d\eta ^\mu d\eta _\mu}$$ $$=-mc\int _a^b {1\over 2} {\color{red}{\delta d\eta ^\mu \cdot d\eta _\mu +d\eta ^\mu \cdot \delta d\eta _\mu} \over \sqrt{d\eta ^\mu d\eta _\mu}} $$

    進階：Thm.4:
    對Scalar變分與上下標無關 回憶度規張量Metric Tensor \(g_{\mu \nu}\) ： $$g_{\mu \nu} =\hat{e} _\mu \cdot \hat{e} _\nu $$ $$g_{\mu \nu} =g_\nu \mu $$ $$g^{\mu \nu} \equiv (g_{\mu \nu} )^{-1}$$ \(g^{\mu \nu} g_{\nu \omega} = \delta ^\mu _\omega \)（Delta funcion，暫時不要跟變分\(\delta\) 搞混）。 度規張量\(g_{\mu \nu}\) 是時空的內稟性質(Intrinsic Property)，與\(x^\mu\) 無關(暫時只考慮狹義相對論，廣義相對論就會有影響)，意思是對\(x^\mu\) 變分與度規\(g_{\mu \nu}\) 無關。度規張量可以用作上下標轉換（Index lowering or raising） $$x^\mu =g^{\mu \nu} x_\nu $$ $$x_\mu =g_{\mu \nu} x^\nu $$ 因為對\(x^\mu\) 變分與度規\(g_{\mu \nu}\) 無關，所以 $$\delta x^\mu =g^{\mu \nu} \delta x_\nu$$ $$\delta x_\mu =g_{\mu \nu} \delta x^\nu $$ 對一個Scalar作變分，例如\(x^\mu y_\mu \)是一個Scalar \(x^\mu y_\mu =x_\mu y^\mu \) $$\delta (x^\mu y_\mu )=\delta x^\mu \cdot y_\mu +x^\mu \cdot \delta y_\mu $$ $$=g^{\mu \nu} \delta x_\nu \cdot g_{\mu \omega} y^\omega +g^{\mu \nu} x_\nu \cdot g_{\mu \omega} \delta y^\omega $$ $$=g^{\mu \nu} g_{\mu \omega} (\delta x_\nu \cdot y^\omega +x_\nu \cdot \delta y^\omega )=g^{\color{red}{\nu \mu}} g_{\mu \omega} \delta (x_\nu y^\omega )$$ $$= \delta ^\nu _\omega \delta (x_\nu y^\omega )=\delta (x_\omega y^\omega )=\delta (x_\mu y^\mu )$$ 同理 $$x^\mu \delta y_\mu =x_\mu \delta y^\mu $$ 所以 $$\color{red}{\delta dx^\mu \cdot dx_\mu +dx^\mu \cdot \delta dx_\mu} $$ $$=\delta dx^\mu \cdot dx_\mu +dx_\mu \cdot \delta dx^\mu $$ $$=2\delta dx^\mu \cdot dx_\mu $$
    $$\delta S_P=-mc\int _a^b {1\over 2} {2\delta d\eta ^\mu\cdot d\eta _\mu \over \sqrt{d\eta ^\mu d\eta _\mu} } $$ $$= -mc\int _a^b {\delta d\eta ^\mu \cdot d\eta _\mu \over cd\tau}$$ $$ =-m\int _a^b \delta d\eta ^\mu \cdot U_\mu $$ 利用Thm.1的方法，我們將\(\delta dx^\mu \)對調成\(d\delta x^\mu\) ，並作分部積分 $$\delta S_P=-m\int _a^b U_\mu d\delta \eta ^\mu $$ $$=\color{red}{ -\left[ U_\mu \delta \eta ^\mu \right]\Big| _a^b}+m\int _a^b dU_\mu \delta \eta ^\mu$$ 邊界項因為變分邊界\(\delta \eta ^\mu (a)=\delta \eta ^\mu (b)=0\)，後面那一項利用Thm.3同乘同除\(d\tau\) 不影響變分 $$\delta S_P=m\int _a^b dU_\mu \delta \eta ^\mu $$ $$ =\int _a^b {m (dU_\mu )\over d\tau} \delta \eta ^\mu d\tau $$ 所以對Free particle而言，\(\delta S_P=0\)使得 \(m {dU_\mu \over d\tau} =0\) 觀察\(\mu =1\sim 3\) $$m {d\overrightarrow{v}\over d\tau} =0$$ Free particle沒有加速度，保持等速運動。

  3. Charge Particle與EM Field作用下的變分與運動方程

    4. 在這一部分中，我們想探討一個Charge Particle在給定的EM Field下如何運動？（注意喔，給定的EM Field表示我們不對EM Field作變分）。相對論性電磁學下我們會寫下4-Potential \(A= A^\mu \hat{e} _\mu =\left(\phi,\overrightarrow{A}\right)\)，在這邊採用高斯制（Gaussian unit），而Charge Particle交互作用的Action \(S_{PF}\)會寫成 $$S_{PF}=\int _a^b -{e \over c} A_\mu d\eta ^\mu $$ 完整的描述Charge Particle運動即為 $$S=S_P+S_{PF}=\int _a^b -mc^2 d\tau +\int _a^b -{e\over c} A_\mu d\eta ^\mu $$ 在這邊，我們考慮Charge Particle在時空中的路徑作\(\eta ^\mu\) 變分 $$\eta ^\mu \to \eta ^\mu +\delta \eta ^\mu $$ 雖然我們沒有對EM Field \(A^\mu\) 作變分，但是走不同路徑感受到的位能是不一樣的，所以Action走不同的路徑會有不同的\(A^\mu \)（意思是\(A^\mu \) 的變化來自於路徑 \(\eta ^\mu\) 不同，而不是對\(A^\mu\) 作變分） $$A^\mu (\eta ^\mu )\to A^\mu (\eta ^\mu +\delta \eta ^\mu )=A^\mu (\eta ^\mu )+\delta A^\mu $$

    取代文字
    取代文字
    我們計算\(\delta S_{PF}\)如何變分： $$\delta S_{PF}=\delta \int _a^b -{e\over c} A_\mu d\eta ^\mu $$ $$ =-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu -{e\over c} \int _a^b A_\mu \cdot \delta d\eta ^\mu $$ 利用Thm.1的方法，我們將\(\delta d\eta ^\mu \)對調\(d\delta \eta ^\mu \) $$\delta d\eta ^\mu =d\delta \eta ^\mu $$ 並作分部積分，邊界項會消失 $$\delta S_{PF}=-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu -{e\over c} \int _a^b A_\mu \cdot d\delta \eta ^\mu $$ $$ =-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu \color{red}{ -\left[{e\over c} A_\mu \cdot \delta \eta ^\mu \right] \Big|_a^b}+{e\over c} \int _a^b dA _\mu \cdot \delta \eta ^\mu $$ 利用Thm.3同乘同除\(d\tau \)不影響變分 $$\delta S_{PF}=-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu +{e\over c} \int _a^b dA _\mu \cdot \delta \eta ^\mu $$ $$ =-{e\over c} \int _a^b \delta A_\mu \cdot {d\eta ^\mu \over \color{red}{d\tau}} \color{red}{d\tau} +{e\over c} \int _a^b {dA _\mu \over \color{red}{d\tau}} \color{red}{d\tau} \cdot \delta \eta ^\mu $$ 因為 $$\delta A_\mu ={\partial A_\mu \over \partial x ^\nu } \delta \eta ^\nu $$
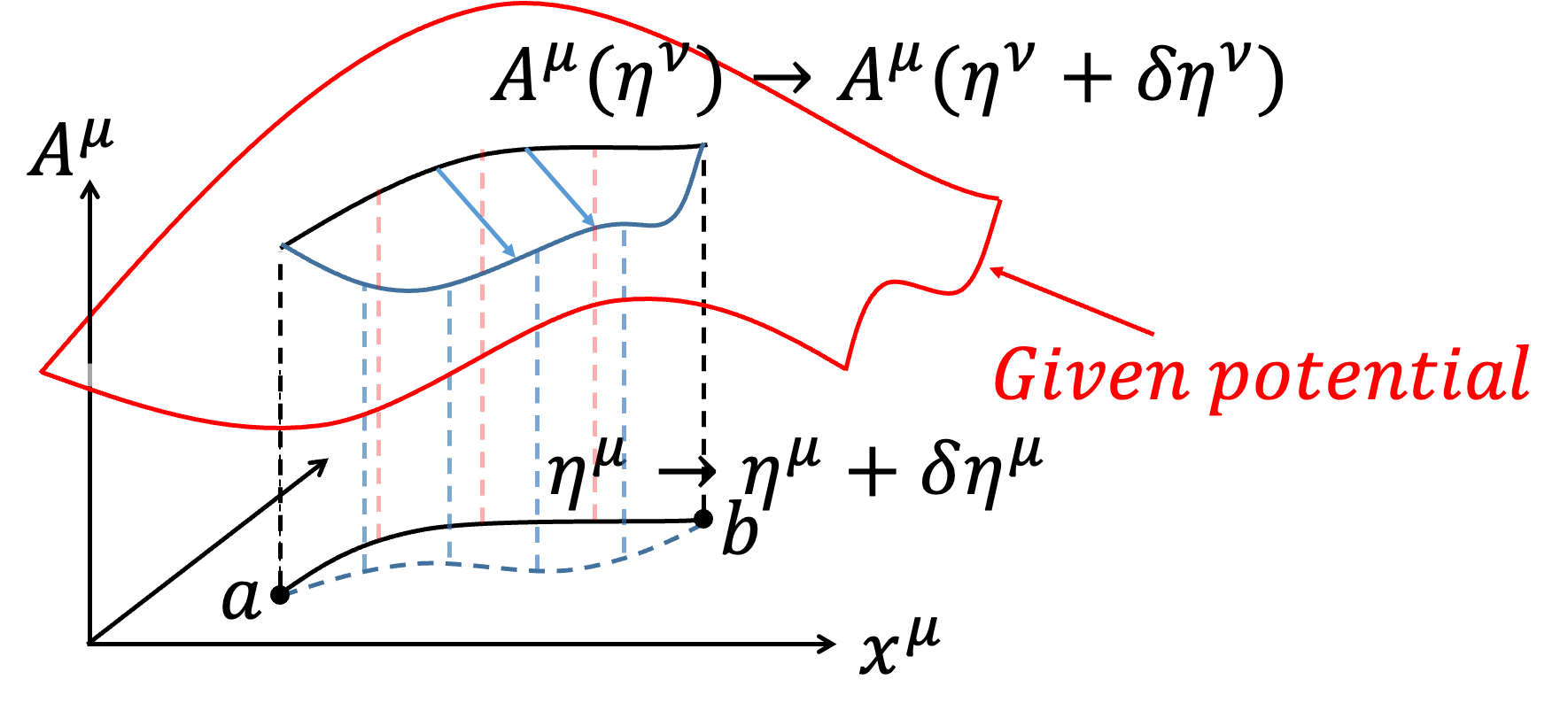    $${dA_\mu \over d\tau} ={\partial A_\mu \over \partial x^\nu } {d\eta ^\nu \over d\tau} ={\partial A_\mu \over \partial x^\nu } U^\nu $$ 代入得到 $$\delta S_{PF}=-{e\over c} \int _a^b {\partial A_\mu \over\partial x^\nu } \delta \eta ^\nu \cdot u^\mu d\tau +{e\over c} \int _a^b {\partial A_\mu \over \partial x^\nu } U^\nu d\tau \cdot \delta \eta ^\mu$$ $$=-{e\over c} \int _a^b (\partial _\nu A_\mu ) u^\mu \delta \eta ^\nu d\tau +{e\over c} \int _a^b \left(\partial _\nu A_\mu \right) U^\nu \delta \eta ^\mu d\tau $$ 我們想要把變分\(\delta \eta ^\nu \)和\(\delta \eta ^\mu\) 一起提出來，但是上標不一樣。但因為每一項\(\mu\) 、\(\nu\) 都是Dummy index，可以互換\(\mu \leftrightarrow \nu\) ，我們把第一項的\(\mu\) 、\(\nu\)互換，就可以把兩項合併 $$\delta S_{PF}=-{e\over c} \int _a^b \left(\partial _\color{red}{\mu} A_\color{red}{\nu} \right) U^\color{red}{\nu} \delta \eta ^\color{red}{\mu} d\tau +{e\over c} \int _a^b (\partial _\nu A_\mu ) U^\nu \delta \eta ^\mu d\tau $$ $$=-{e\over c} \int _a^b (\partial _\mu A_\nu -\partial _\nu A_\mu ) U^\nu \delta \eta ^\mu d\tau $$ 完整考慮Charge Particle在EM Field中的運動 $$\delta S=\delta S_P+\delta S_{PF}=0$$ 所以 $$\delta S_P+\delta S_{PF}=\int _a^b m {dU_\mu \over d\tau} \delta \eta ^\mu d\tau -{e\over c} \int _a^b \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu \delta \eta ^\mu d\tau $$ $$=\int _a^b \left[m {dU_\mu \over d\tau} -{e\over c} \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu \right] \delta \eta ^\mu d\tau =0$$ 會得到 $$m {dU_\mu \over d\tau} -{e\over c} \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu =0$$
    $$m {dU_\mu \over d\tau} ={e\over c} \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu \equiv {e\over c} F_{\mu \nu} U^\nu $$ 我們定義電磁張量Electromagnetic Tensor $$F_{\mu \nu} =\partial _\mu A_\nu -\partial _\nu A_\mu $$ 電場\(\overrightarrow{E}\)、磁場\(\overrightarrow{B}\)與\(\phi\)、\(\overrightarrow{A}\)的關係（高斯制） $$ \overrightarrow{E}=-\nabla \phi-{1\over c} {\partial \overrightarrow{A}\over \partial t}$$ $$\overrightarrow{B}=\nabla \times \overrightarrow{A} $$ 其中 $$A_\nu \to \left(\phi,-A_x,-A_y,-A_z \right)$$ $$\partial _\mu \to \left({\partial \over \partial x^0},{\partial \over \partial x^1 },{\partial \over \partial x^2},{\partial \over \partial x^3 }\right)=\left({\partial \over \partial ct},{\partial \over \partial x },{\partial \over \partial y},{\partial \over \partial z }\right)$$ 可以計算 $$F_{\mu \nu} =\partial _\mu A_\nu -\partial _\nu A_\mu =\left(\begin{matrix}0 & E_x & E_y & E_z\\ -E_x & 0 & -B_z & B_y \\ -E_y & B_z & 0 & -B_x \\ -E_z & -B_y & B_x & 0 \end{matrix}\right)$$ $$F^{\mu \nu} =\partial ^\mu A^\nu -\partial ^\nu A^\mu =\left(\begin{matrix}0 & -E_x & -E_y & -E_z\\ E_x & 0 & -B_z & B_y \\ E_y & B_z & 0 & -B_x \\ E_z & -B_y & B_x & 0 \end{matrix}\right)$$

  4. 4-Volume \(d^4 x\)與Lagrangian Density \(\mathcal{L}\)

    5. 因為時空在相對論下是等價的，利用相對性原理（Principle of Relativity）和最小作用量原理（Principle of least action）的要求，物理學家會將Action S寫成Scalar的形式，從而保證在任何作標系下\(\delta S=0\)。剛剛我們所列下來的Action： $$S_P=-mc^2 \int _a^b d\tau $$
    $$S_{PF}=-{e\over c} \int _a^b A_\mu dx^\mu $$
    $$S=S_P+S_{PF}=-mc^2 \int _a^b d\tau -{e\over c} \int _a^b A_\mu dx^\mu $$ $$=\int _a^b -\gamma mc^2-\gamma e \phi+{e\over c} \overrightarrow{A} \cdot \gamma \overrightarrow{v} dt =\int _a^b Ldt$$ 雖然Action都滿足Scalar的要求，但是Lagrangian L本身並不是Scalar，因為換到不同座標系下會不一樣，物理學家於是想要進一步將Lagrangian L改寫成Scalar的形式。我們定義4-Volume \(d^4 x=dc\tau dV=dc\tau dxdydz\)，並將原本的Action改寫 $$S_P=-mc^2 \int _a^b d\tau =-\int \rho_m dV c^2 \int _a^b d\tau $$ $$=-∬ \rho_m cdc\tau dV =\int -\rho_m cd^4 x $$
    $$S_{PF}=-{e\over c} \int _a^b A_\mu dx^\mu =-{\int \rho_e dV \over c} \int _a^b A_\mu {dx^\mu \over d\tau} d\tau $$ $$=-{1 \over c} ∬ \rho_e A_\mu u^\mu d\tau dV =-{1 \over c^2} ∬ A_\mu J^\mu dc\tau d^4 x $$ $$=-{1 \over c^2} \int A_\mu J^\mu d^4 x $$ 其中，4-current density \(J=J^\mu \hat{e} _\mu =\rho_e u^\mu \hat{e} _\mu\) 。特別的是\(d^4 x\)是一個不變量Invariant，所以是一個Scalar。另外在加上EM Field的Action \(S_F\) $$S_F=-{1 \over 16\pi c} \int F_{\mu \nu} F^{\mu \nu} d^4 x $$ $$S=S_P+S_{PF}+S_F$$ $$=\int -\rho_m c-{1\over c^2} A_\mu J^\mu -{1 \over 16\pi c} F_{\mu \nu} F^{\mu \nu} d^4 x$$ $$ \equiv \int \mathcal{L} d^4 x $$ 因為4-Volume \(d^4 x\)是一個Scalar，Action也是一個Scalar，所以\(\mathcal{L}\)也是一個Scalar。\(\mathcal{L}\)我們稱為Lagrangian density，Lagrangian density　\(\mathcal{L}\)在任何座標系下都是Scalar，形式保持不變： $$\mathcal{L}=-\rho_m c-{1\over c^2} A_\mu J^\mu -{1 \over 16\pi c} F_{\mu \nu} F^{\mu \nu} $$

    進階：\(d^4 x\)是一個不變量Invariant
    物理proof
    因為Time dilation 和 Length contraction相反。如果\(\tau\) 、\(\bar{x}\)是proper time和proper length $$t=\gamma \tau $$ $$x={\bar{x} \over \gamma} $$ 所以 $$dctdx=dc\left(\gamma \tau \right)d{\bar{x} \over \gamma }=dc\tau d\bar{x}$$ 數學proof
    回憶Jacobian \(J\) $$dxdy=rdrdθ=J\left(r,\theta\right)drd\theta$$ 其中 $$J\left(r,\theta\right)=\left| \begin{matrix} {\partial x \over \partial r} & {\partial x \over \partial \theta} \\ {\partial y \over \partial r} & {\partial y \over \partial \theta} \end{matrix} \right| =\left| \begin{matrix} {\partial rcos\theta \over \partial r} & {\partial rcos\theta \over \partial \theta} \\ {\partial rsin\theta \over \partial r} & {\partial rsin\theta \over \partial \theta} \end{matrix} \right| $$ $$=\left| \begin{matrix} { cos\theta} & { -rsin\theta} \\ { sin\theta} & { rcos\theta} \end{matrix} \right|=r $$ 同理 $$dc\bar{t} d\bar{x}=J\left(ct,x\right)dctdx=\left| \begin{matrix} {\partial c\bar{t} \over \partial ct} & {\partial c\bar{t} \over \partial x} \\ {\partial \bar{x} \over \partial ct} & {\partial \bar{x} \over \partial x} \end{matrix} \right|dctdx$$ 回憶勞倫茲轉換 $$c\bar{t} =\gamma (ct-\beta x)$$ $$\bar{x}=\gamma (x-\beta ct)$$ 代回去計算 $$dc\bar{t} d \bar{x}=\left| \begin{matrix} \gamma & -\beta \gamma \\ -\beta \gamma & \gamma \end{matrix} \right|dctdx $$ $$=\gamma ^2 (1-\beta ^2 )dctdx=dctdx$$ 所以\(d^4 x\)在勞倫茲轉換下是一個不變量。

  5. Maxwell's equations

    6. 在這一部分，我們在給定Source下，討論EM Field的分佈（給定Source下表示我們不對Source下的分佈\(\eta ^\mu\) 作變分）。 $$S_{PF}+S_F=\int -\rho_m c-{1\over c^2} A_\mu J^\mu d^4 +\int-{1 \over 16\pi c} F_{\mu \nu} F^{\mu \nu} d^4 x$$ 我們想知道EM Field的分佈，所以我們針對\(A^\mu\) 作變分 $$A^\mu \to A^\mu +\delta A^\mu $$ 我們來觀察\(J^\mu \)、\(d^4 x\)、\(F^{\mu \nu}\) 會不會受到影響？
    取代文字
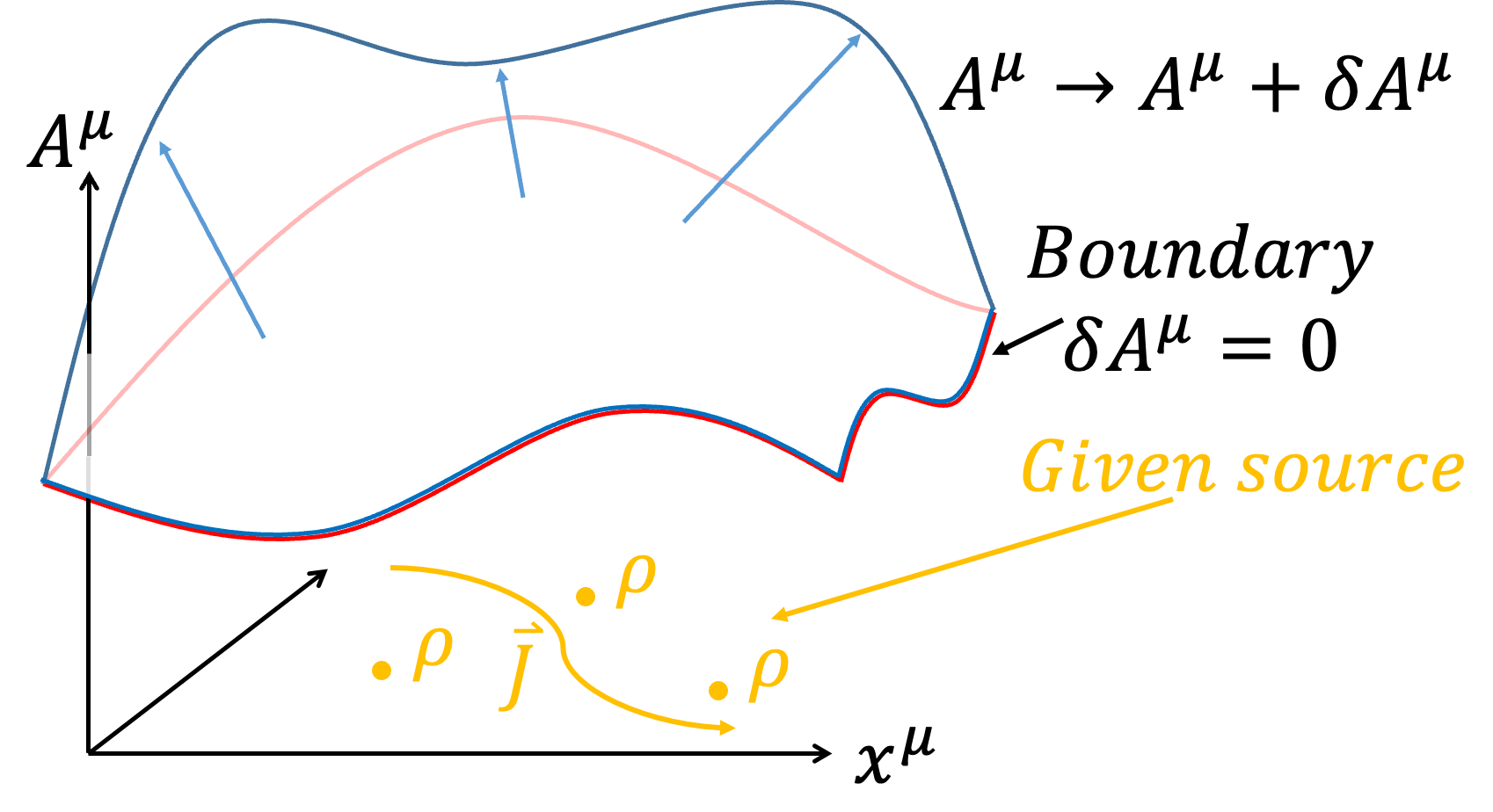
    $$J^\mu =\rho_e {dx^\mu \over d\tau} =J^\mu (x^\nu )$$ $$d^4 x=d^4 x(x^\nu )$$ $$F^{\mu \nu} =\partial ^\mu A^\nu -\partial ^\nu A^\mu =F^{\mu \nu} \left(A^\omega \right)$$ 可見只有電磁張量\(F^{\mu \nu}\) 會受到\(A^\mu \)的變分\(A^\mu \to A^\mu +\delta A^\mu\) 有關 $$F^{\mu \nu} \left(A^\omega \right)\to F^{\mu \nu} (A^\omega +\delta A^\omega )=F^{\mu \nu} \left(A^\omega \right)+\delta F^{\mu \nu} $$ 所以\(S_{PF}\)的變分很簡單 $$\delta S_{PF}=\delta \int -{1 \over c^2} A_\mu J^\mu d^4 x$$ $$ =-{1 \over c^2} \int \delta A_\mu \cdot J^\mu d^4 x $$ 至於\(S_F\)的變分就稍嫌複雜 $$S_F=-{1 \over 16 \pi c} \int F_{\mu \nu} F^{\mu \nu} d^4 x$$ $$\delta S_F=-{1 \over 16 \pi c} \delta \int F_{\mu \nu} F^{\mu \nu} d^4 x =-{1 \over 16 \pi c} \int \delta F_{\mu \nu} \cdot F^{\mu \nu} +F_{\mu \nu} \cdot \delta F ^{\mu \nu} d^4 x $$ 利用Thm.4: 對Scalar變分與上下標無關，所以\(\delta F_{\mu \nu} \cdot F^{\mu \nu} =F_{\mu \nu} \cdot \delta F ^{\mu \nu}\) ，會有兩倍 $$\delta S_F=-{1 \over 16 \pi c} \int 2\delta F_{\mu \nu} \cdot F^{\mu \nu} d^4 x =-{1 \over 8 \pi c} \int \delta F_{\mu \nu} \cdot F^{\mu \nu} d^4 x $$ $$=-{1 \over 8 \pi c} \int \delta (\partial _\mu A_\nu -\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ $$=-{1 \over 8 \pi c} \int \delta (\partial _\mu A_\nu )\cdot F^{\mu \nu} d^4 x +{1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ 因為每一項\(\mu\) 、\(\nu\) 都是Dummy index，可以互換\(\mu \leftrightarrow \nu \)，我們把第一項的\(\mu\) 、\(\nu\) 互換，就可以把兩項合併 $$\delta S_F=-{1 \over 8 \pi c} \int \delta (\partial _\color{red}{\nu} A_\color{red}{\mu} )\cdot F^\color{red}{\nu \mu} d^4 x +{1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ $$={1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot (-F^\nu \mu +F^{\mu \nu} ) d^4 x $$ 回憶電磁張量 $$F^{\mu \nu} =\partial ^\mu A^\nu -\partial ^\nu A^\mu =\left(\begin{matrix}0 & -E_x & -E_y & -E_z\\ E_x & 0 & -B_z & B_y \\ E_y & B_z & 0 & -B_x \\ E_z & -B_y & B_x & 0 \end{matrix}\right)$$ \(F^{\mu \nu} \)是一個反對稱張量，所以\(F^\nu \mu =-F^{\mu \nu} \) 代回去會多兩倍 $$\delta S_F={1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot (F^\color{red}{\mu \nu} +F^{\mu \nu} ) d^4 x ={1 \over 4 \pi c} \int \delta (\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ 利用Thm.1的方法，我們將\(\delta\) 和\(\partial _\nu \)對調 $$\delta (\partial _\nu A_\mu )=\partial _\nu (\delta A_\mu )$$ $$\delta S_F={1 \over 4 \pi c} \int \partial _\nu (\delta A_\mu )\cdot F^{\mu \nu} d^4 x $$ 利用微分的Chain rule， $$\partial _\nu (\delta A_\mu )\cdot F^{\mu \nu} =\partial _\nu (\delta A_\mu \cdot F^{\mu \nu} )-\delta A_\mu \cdot \partial _\nu (F^{\mu \nu} )$$ 將積分拆成兩項 $$\delta S_F={1 \over 4 \pi c} \int \partial _\nu (\delta A_\mu \cdot F^{\mu \nu} ) d^4 x -{1 \over 4 \pi c} \int \delta A_\mu \cdot \partial _\nu (F^{\mu \nu} ) d^4 x $$

    回憶Divergence theorem $$\int \nabla \cdot \overrightarrow{F}dV =∮ \overrightarrow{F}\cdot d\overrightarrow{S} $$ 一個體積分，可以改寫成對體表面的面積分。寫成Levi-Civita symbol $$\int \partial _\nu F^\nu dV =∮ F^\nu dS_\nu $$
    所以第一項利用Divergence theorem，但是Boundary上的\(\delta A_\mu =0\)，所以 $${1 \over 4 \pi c} \int \partial _\nu (\delta A_\mu \cdot F^{\mu \nu} ) d^4 x ={1 \over 4 \pi c} ∮ \delta A_\mu \cdot F^{\mu \nu} dS_\nu =0$$ 所以 $$\delta S_F=-{1 \over 4 \pi c} \int \partial _\nu (F^{\mu \nu} )\cdot \delta A_\mu d^4 x $$ 合併\(\delta S_{PF}+\delta S_F\) $$\delta S_{PF}+\delta S_F=-{1 \over c^2} \int J^\mu \cdot \delta A_\mu d^4 x -{1 \over 4 \pi c} \int \partial _\nu (F^{\mu \nu} )\cdot \delta A_\mu d^4 x$$ $$=\int \left[-{1 \over c^2} J^\mu -{1 \over 4 \pi c} \partial _\nu F^{\mu \nu} \right]\delta A_\mu d^4 x =0$$ 會得到 $$-{1 \over c^2} J^\mu -{1 \over 4 \pi c} \partial _\nu F^{\mu \nu} =0$$ $$\partial _\nu F^{\mu \nu} =-{4\pi \over c} J^\mu $$
    Recall Maxwell's equation in Gaussian Unit $$ \nabla \cdot \overrightarrow{E}=4\pi \rho_e$$ $$ \nabla \cdot \overrightarrow{B}=0)$$ $$ \nabla ×\overrightarrow{E}=-{1 \over c} {\partial \overrightarrow{B} \over \partial t}$$ $$ \nabla ×\overrightarrow{B}={4\pi \over c} \overrightarrow{J}+{1 \over c} {\partial \overrightarrow{E} \over \partial t }$$
    $$\partial _\nu F^{\mu \nu} =-{4\pi \over c} J^\mu \to \left( \begin{matrix} \nabla \cdot \overrightarrow{E}=4\pi \rho_e \\ \nabla ×\overrightarrow{B}={4\pi \over c} \overrightarrow{J}+{1 \over c} {\partial \overrightarrow{E}\over \partial t} \end{matrix}\right)$$
    $$F_{\mu \nu} =\partial _\mu A_\nu -\partial _\nu A_\mu $$ 電磁張量有特別的關係式(Bianchi identity) $$\partial _\omega F_{\mu \nu} +\partial _\mu F_{\nu \omega} +\partial _\nu F_{\omega \mu} =\partial _{[\omega} F_{\mu \nu ]} =0$$ 展開 $$\partial _\omega (\partial _\mu A_\nu -\partial _\nu A_\mu )+\partial _\mu (\partial _\nu A_\omega -\partial _\omega A_\nu )+\partial _\nu (\partial _\omega A_\mu -\partial _\mu A_\omega )=0$$ $$\partial _\omega \partial _\mu A_\nu -\partial _\omega \partial _\nu A_\mu +\partial _\mu \partial _\nu A_\omega -\partial _\mu \partial _\omega A_\nu +\partial _\nu \partial _\omega A_\mu -\partial _\nu \partial _\mu A_\omega =0$$ 這條關係式會得到
    $$ \partial _\omega F_{\mu \nu} +\partial _\mu F_\nu \omega +\partial _\nu F_\omega \mu =0 \to \left( \begin{matrix} \nabla \cdot \overrightarrow{B}=0 \\ \nabla ×\overrightarrow{E}=-{1 \over c} {\partial \overrightarrow{B} \over \partial t} \end{matrix}\right)$$

  6. 電磁學中的規範不變性Gauge Invariance

    7. 在電磁學中，我們定義Potential \(\phi\)、\(\overrightarrow{A}\)和電場\(\overrightarrow{E}\)、磁場\(\overrightarrow{B}\)的關係： $$ \overrightarrow{E}=- \nabla \phi -{1 \over c} {\partial \overrightarrow{A}\over \partial t}$$ $$\overrightarrow{B}= \nabla ×\overrightarrow{A} $$ 但Potential \(\phi\) 、\(\overrightarrow{A}\)不唯一，可以引入一個Gauge function \(G(ct,\overrightarrow{x} )\) $$\bar{\phi} =\phi +{1 \over c} {\partial G \over \partial t}$$ $$\overrightarrow{\bar{A}}=\overrightarrow{A}- \nabla G$$ 一樣保持電場\(\overrightarrow{E}\)、磁場\(\overrightarrow{B}\)不變 $$\overrightarrow{\bar{E}}=- \nabla \bar{\phi}-{1 \over c} {\partial \overrightarrow{\bar{A}}\over \partial t}$$ $$=- \nabla \phi - \color{red}{\nabla {1 \over c} {\partial G \over \partial t}}-{1 \over c} {\partial \overrightarrow{A}\over \partial t}+\color{red}{{1 \over c} {\partial ( \nabla G)\over\partial t}}$$ $$=- \nabla \phi -{1 \over c} {\partial \overrightarrow{A}\over \partial t}=\overrightarrow{E}$$
    $$\overrightarrow{\bar{B}}= \nabla ×\overrightarrow{\bar{A}}= \nabla ×\overrightarrow{A}- \nabla × \nabla G= \nabla ×\overrightarrow{A}=\overrightarrow{B} $$

    Note \(\nabla × \nabla G=0\) $$( \nabla × \nabla G)_i=\varepsilon _{ijk} \partial _j \partial _k G$$ $$={1 \over 2} \varepsilon _{ijk} \partial _j \partial _k G+{1 \over 2} \varepsilon _{ijk} \partial _j \partial _k G$$ $$={1 \over 2} \varepsilon _{ijk} \partial _j \partial _k G+{1 \over 2} \varepsilon _{i\color{red}{kj}} \partial _\color{red}{k} \partial _\color{red}{j} G$$ $$={1 \over 2} \varepsilon _{ijk} \partial _j \partial _k G \color{red}{-}{1 \over 2} \varepsilon _{i\color{red}{jk}} \partial _j \partial _k G=0$$
    在相對論中，上述的操作可以寫為4-Potential的形式： $$(\bar{\phi},\overrightarrow{\bar{A}} )=(\phi ,\overrightarrow{A} )+(\partial _{ct} G,- \nabla G)=(\phi ,\overrightarrow{A} )+(\partial _{ct},- \nabla )G$$ 回憶 $$\partial ^\mu =(\partial _{ct},- \nabla )$$ 故寫成 $$\bar{A} ^\mu =A^\mu +\partial ^\mu G$$
    Coulomb gauge condition：非相對論性Non-relativistic $$ \nabla \cdot \overrightarrow{A}=0$$
    Lorenz gauge condition：相對論性，滿足Lorentz transformation $$ \nabla \cdot \overrightarrow{A}+{1 \over c} {\partial \phi \over \partial t}=0$$ 寫成Scalar form $$\partial _\mu A^\mu =0$$ 所以滿足相對論轉換。
    剛剛已經寫下電場\(\overrightarrow{E}\)、磁場\(\overrightarrow{B}\)在加入Gauge之下保持不變 $$\overrightarrow{\bar{E}}=\overrightarrow{E}$$ $$\overrightarrow{\bar{B}}=\overrightarrow{B}$$ 這其實說明，\(F^{\mu \nu}\) 也在加入Gauge之下保持不變： $$ \bar{F} ^{\mu \nu} =F^{\mu \nu} $$ 當然我們也可以寫下證明 $$\bar{F} ^{\mu \nu} =\partial ^\mu \bar{A} ^\nu -\partial ^\nu \bar{A} ^\mu$$ $$=\partial ^\mu (A^\nu +\partial ^\nu G)-\partial ^\nu (A^\mu +\partial ^\mu G)$$ $$=\partial ^\mu A^\nu +\color{red}{\partial ^\mu \partial ^\nu G}-\partial ^\nu A^\mu -\color{red}{\partial ^\nu \partial ^\mu G}$$ $$=\partial ^\mu A^\nu -\partial ^\nu A^\mu =F^{\mu \nu} $$

  7. 規範不變與Action的變分

    8. 這部分要討論的是，加入Gauge不會改變Action的變分，意味著運動方程不會受到Gauge的改變，也代表Gauge Invariance。當加入Gauge時。： $$ \bar{A} ^\mu =A^\mu +\partial ^\mu G$$ 我們來觀察一下Action \(S=S_P+S_{PF}+S_F\)有誰會受到影響： $$S_P=-mc^2 \int _a^b d\tau =\int -\rho_m cd^4 x $$ $$S_{PF}=-{e\over c} \int _a^b A_\mu dx^\mu =-{1 \over c^2} \int A_\mu J^\mu d^4 x $$ $$S_F=\int -{1 \over 16 \pi c} F_{\mu \nu} F^{\mu \nu} d^4 x $$ 因為剛剛已經證明，\(F^{\mu \nu}\) 不受到Gauge的影響，而\(S_P\)沒有\(A^\mu\) 相關，所以唯一受到影響的是\(S_{PF}\) $$\bar{S}_{PF}=-{e\over c} \int _a^b \bar{A} _\mu dx^\mu =-{1 \over c^2} \int \bar{A} _\mu J^\mu d^4 x $$ 針對\(\bar{S}_{PF}\)變分 $$\delta \bar{S}_{PF}=-{1 \over c^2} \delta \int \bar{A} _\mu J^\mu d^4 x =-{1 \over c^2} \delta \int A_\mu J^\mu d^4 x \color{red}{-{1 \over c^2} \delta \int \partial _\mu G \cdot J ^\mu d^4 x }$$ 將後面那一項利用微分的Chain rule $$\partial _\mu G \cdot J ^\mu =\partial _\mu (GJ^\mu )-G\partial _\mu J^\mu $$ $$\delta \bar{S}_{PF}=-{1 \over c^2} \delta \int A_\mu J^\mu d^4 x \color{red}{-{1 \over c^2} { \delta \int \partial _\mu \left(GJ^\mu \right) d^4 x + {1 \over c^2} \delta \int G\partial _\mu J^\mu d^4 x} } $$ 中間項利用Divergence theorem改寫成 $$\delta \bar{S}_{PF}=-{1 \over c^2} \delta \int A_\mu J^\mu d^4 x \color{red}{-{1 \over c^2} {\delta \left[ ∮ GJ^\mu dS_\mu \right]}{ +{1 \over c^2} \delta \int G \left[\partial _\mu J^\mu \right] d^4 x }}$$ 中間項因為Boundary上的變分為0，所以中間項為0： $$\color{red}{\delta \left[∮ GJ^\mu dS_\mu \right]=0}$$ 最後一項回憶（由實驗觀察到的）連續性方程Continuity equation $${\partial \rho_e \over \partial t}+ \nabla \cdot \overrightarrow{J}=0$$ 寫成相對論性 $$\partial _\mu J^\mu =0$$ 導致最後一項也為0 $$\color{red}{\delta \int G \left[\partial _\mu J^\mu \right] d^4 x =0}$$ 所以 $$\delta \bar{S}_{PF}=-{1 \over c^2} \delta \int A_\mu J^\mu d^4 x =\delta S_{PF}$$ 這表示加入Gauge不會改變Action的變分，整套物理滿足Gauge Invariance。

  8. 淺談Gauge Invariance和Continuity equation

    9. 淺談Gauge Invariance和Continuity equation 剛剛我們的推導中，利用連續性方程Continuity equation得到Action的變分滿足規範不變性。而Continuity equation對應到的是電荷守恆Charge conservation。在物理的發展後期，物理學開始反其道而行，當我們要求Action滿足規範不變性，便可以得到Continuity equation和Charge conservation。變分的過程完全一樣，唯一的差別在於我們強迫 $${1 \over c^2} \delta \int G[\partial _\mu J^\mu ] d^4 x =0$$ 以保證變分結果不受到Gauge影響，這就可以得到 $$\partial _\mu J^\mu =0$$ 學到這部分，大概可以了解到，物理學家常常說Action強大的地方，我們可以寫下Action就可以得到實驗上所有得到的實驗方程。但真正Action的發展上，都必須要有實驗先得到部分或全部的運動方程，物理學家經由一些物理論證，猜出Action的形式，再藉由Action去得到其餘更深刻的物理。由於古典電磁學的發展很全面，電磁學裡面的所有方程都已經經由實驗得到，所以在推導Action的變分得到\(F^{\mu \nu}\) 或Maxwell's equations就覺得很像看著答案寫問題。不過物理的發展上我們實驗上得到電荷守恆，物理學家改寫成Action的描述，可以諾特定理Noether's theorem很嚴謹的連結電荷守恆和規範不變性的關係。這就像是過去從牛頓力學經由虛功原理可以得到Action的描述（Hamilton principle），物理學家便可以反過來從Action得到牛頓力學，但是Action整套東西還可以來描述電磁學，甚至是後來的量子力學（Feynman的Path integral），Action對於推廣物理有至關重要的地位。

  9. Impossibility of \(A_\mu A^\mu\) if keeping gauge invariance

    10. 如果保持規範不變的話，我們可以論證Action不會有\(A_\mu A^\mu \)項，因為\(A^\mu\) 的變分\(A^\mu \to A^\mu +\delta A^\mu \)會導致運動方程變化。 $$S=-{1 \over c^2} \int A_\mu A^\mu d^4 x $$ 加入Gauge \(\partial ^\mu G\) $$ \bar{A} ^\mu =A^\mu +\partial ^\mu G$$ 展開Action $$\bar{S}=-{1 \over c^2} \int \bar{A} _\mu \bar{A} ^\mu d^4 x $$ $$=-{1 \over c^2} \int (A_\mu +\partial _\mu G)(A^\mu +\partial ^\mu G) d^4 x $$ $$=-{1 \over c^2} \int A_\mu A^\mu d^4 x -{1 \over c^2} \int 2A^\mu \cdot \partial _\mu Gd^4 x -{1 \over c^2} \int \partial _\mu G\cdot \partial ^\mu Gd^4 x $$ 因為Gauge \(\partial ^\mu G\)獨立於4-Potential \(A^\mu\) ，\(A^\mu\) 的變分\(A^\mu \to A^\mu +\delta A^\mu\) 不影響\(\partial ^\mu G\)。我們比較對\(S\)變分和對\(\bar{S}\)變分的差異：
    對\(S\)變分 $$\delta S=-{1 \over c^2} \delta \int A_\mu A^\mu d^4 x$$ $$ =-{2 \over c^2} \int A_\mu \delta A^\mu d^4 x$$
    對\(\bar{S}\)變分 $$\delta \bar{S}=-{1 \over c^2} \delta \int A_\mu A^\mu d^4 x -{1 \over c^2} \delta \int 2A_\mu \partial ^\mu Gd^4 x -\color{red}{0（\partial ^\mu G沒有變分）}$$ 第一項就是原本的變分 $$\delta \bar{S}=-{2 \over c^2} \int A_\mu \delta A^\mu d^4 x -{2 \over c^2} \delta \int A^\mu \cdot \partial _\mu Gd^4 x $$ $$=-{2 \over c^2} \int (A_\mu +\partial _\mu G)\delta A^\mu d^4 x $$ 比對後會發現兩者不一樣，會導致規範不變被破壞。如果我們希望保持規範不變性，那就不會出現\(A_\mu A^\mu\) 。當然，也許某一天實驗發現規範不變性是錯誤的，那有可能可以引入\(A_\mu A^\mu \)項。

  10. 淺談量子場論中的\(A_\mu A^\mu\) -光子質量

    11. 本篇內容主要在古典範疇討論，在此簡單討論一下\(A_\mu A^\mu \)在量子場論中對應到的是光子質量。Klein–Gordon equation描述自旋整數的粒子，由來簡單的從相對論出發，根據4-momentum： $$P_\mu P^\mu =m^2 c^2$$ 量子場論與古典的關係其中一點就是所有物理量都改寫成算符(operator)作用到wave function \(\phi\) $$\hat{P} _\mu \hat{P} ^\mu \phi =m^2 c^2 \phi $$ 量子場論中動量算符為 $$\hat{P} ^\mu =i\hbar \partial ^\mu $$ 代入 $$(i\hbar \partial _\mu )(i\hbar \partial ^\mu )\phi =m^2 c^2 \phi $$ $$-\hbar ^2 \partial _\mu \partial ^\mu \phi =m^2 c^2 \phi $$ 得到Klein–Gordon equation $$(\hbar ^2 \partial _\mu \partial ^\mu +m^2 c^2 )\phi =0$$ 如果設\(\hbar =c=1\)（普朗克單位制或自然單位制） $$(□+m^2 )\phi =0$$ 就是常見的形式。在量子場論中描述Spin 1 massive particle的Lagrangian dendity: $$L=-{1 \over 2} \partial _\mu A_\nu \partial ^\mu A^\nu +{1 \over 2} m^2 A_\nu A^\nu (採用\hbar =c=1)$$ 對\(\delta A^\nu \)變分滿足 $$\partial ^\mu \left({\partial L \over \partial \left(\partial ^\mu A^\nu \right)} \right)-{\partial L\over \partial A^\nu }=0$$ 得到 $$-\partial ^\mu (\partial _\mu A_\nu )-m^2 A_\nu =0\to \partial ^\mu \partial _\mu A_\nu +m^2 A_\nu =0$$ $$(□+m^2 ) A_\nu =0$$ 就得到Klein–Gordon equation描述Spin 1 massive particle的EoM。可以看到\(A_\nu A^\nu\) 對應到的是光子質量。不過，正確描述Spin 1 massless particle的Lagrangian dendity並不是\(\mathcal{L}=-{1 \over 2} \partial _\mu A_\nu \partial ^\mu A^\nu\) ，而是 $$\mathcal{L}=-{1\over 4} F_{\mu \nu} F^{\mu \nu} $$ 後續涉及到光子無質量造成的一些自由度問題，會需要一些技術細節將4-potential的四個自由度消除兩個，以對應到光子只有兩個偏振方向，就不再此討論。

  11. 連續場與波動方程

    12. 取代文字
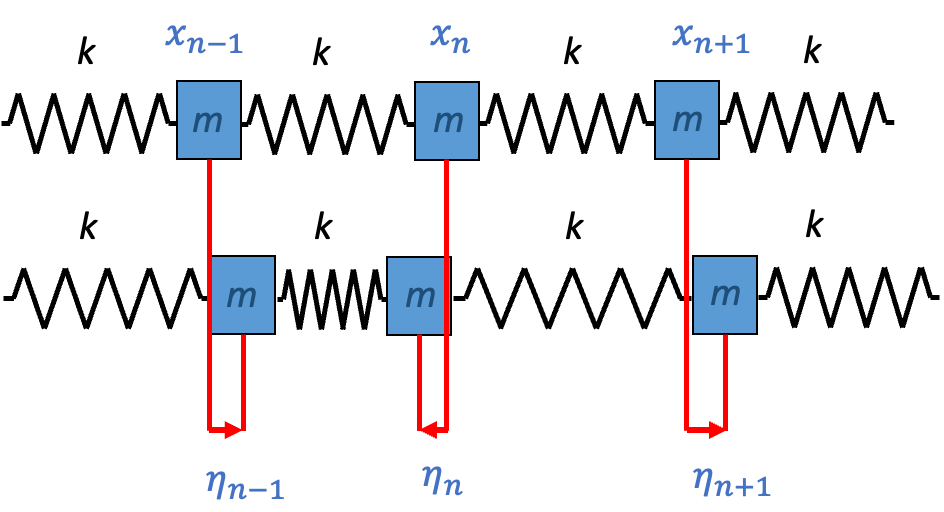
    從單質點進入到連續場之中，物理學家是利用串聯無窮多的簡諧振子去描述一個連續場。針對無窮多的簡諧振子，可以寫下Lagrangian $$\mathcal{L}=∑_n^∞ {1 \over 2} m\eta ̇_n-{1 \over 2} k(\eta _n-\eta _(n-1) )^2 $$ 其中\eta _n是位置n的振幅，\eta ̇_n是位置n的振盪的速度。
    取代文字
    進入到連續場時，Lagrangian為 $$\mathcal{L}=\int {1 \over 2} \rho\left({\partial \eta \over\partial t}\right)^2-{1 \over 2} Y\left({\partial \eta \over\partial x}\right)^2 dx $$ 其中\(\rho\)為質量密度、\(Y\)為楊氏係數。
    取代文字
    在三維Lagrangian為 $$\mathcal{L}=\int {1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2 dV$$ 可以直接看出Lagrangian dendity \(\mathcal{L}={1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2\)。一樣的，我們可以利用Variational principle得到連續場的運動方程。作用量Action為 $$S=\int Ld^4 x =\int {1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2 d^4 x $$ 將場振幅做變分 \(\eta (x^\mu )\to \eta (x^\mu )+\delta \eta (x^\mu )\)，Action變化要為極值： $$\delta S=\delta \int {1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2 d^4 x $$ $$=\int \rho\partial _t \eta *\delta (\partial _t \eta )-Y \nabla \eta *\delta ( \nabla \eta ) d^4 x $$ 將變分和微分交換 $$=\int \rho\partial _t \eta \partial _t (\delta \eta )-Y \nabla \eta \nabla (\delta \eta ) d^4 x $$ $$=\int \rho\partial _t \eta \partial _t (\delta \eta ) d^4 x -\int Y \nabla \eta \nabla (\delta \eta ) d^4 x $$ $$=\int \partial _t (\rho\partial _t \eta \delta \eta ) d^4 x -\int \partial _t (\rho\partial _t \eta )*\delta \eta d^4 x -\int \nabla (Y \nabla \eta \delta \eta ) d^4 x +\int \nabla (Y\eta )*\delta \eta d^4 x $$ $$=\left[-\int \partial _t (\rho\partial _t \eta )*\delta \eta d^4 x +\int \nabla (Y\eta )*\delta \eta d^4 x \right]+\left[\int \partial _t (\rho\partial _t \eta \delta \eta ) d^4 x -\int \nabla (Y \nabla \eta \delta \eta ) d^4 x \right]$$ 後面為邊界項，利用Integral by part $$=-\int \left[\rho\partial _t^2 \eta -Y \nabla ^2 \eta \right]*\delta \eta d^4 x +\left[\int \rho\partial _t \eta \delta \eta d^3 x \Big|_{t_1}^{t_2}- \int Y \nabla \eta \delta \eta d^3 x \Big|_{\partial x,\partial y,\partial z} \right]$$ $$=-\int [\rho\partial _t^2 \eta -Y \nabla ^2 \eta ]*\delta \eta d^4 x +0$$ 因為\(\delta \eta\) 為任意，得到 $$\rho\partial _t^2 \eta -Y \nabla ^2 \eta =0$$ $$ \nabla ^2 \eta ={\rho \over Y} \partial _t^2 \eta $$ 令\(v=\sqrt{{Y\over \rho}}\) $$\nabla ^2 \eta ={1\over v^2} \partial _t^2 \eta $$ 即波動方程。

  12. 古典場論

    13. 在古典場論中，物理學將連續場的振幅\(\eta\) 推廣到古典場的物理量，可以是純量場\(\phi\) 、向量場\(V^\mu\) 、張量場\(T^{\mu\nu}\)等等。先可慮簡單的純量場\(\phi =\phi (x^\mu )\)是時空函數，通過Variational principle找到\(\phi\) 的EoM。先寫下Action，假設Lagrangian dendity \(\mathcal{L}\)是\(\phi\) ,\(\partial _\mu \phi\) 的函數，並通過\(\phi \to \phi +\delta \phi \)的變分 $$S=\int \mathcal{L}[\phi ,\partial _\mu \phi ] d^4 x $$ $$\phi \to \phi +\delta \phi 、\partial _\mu \phi \to \partial _\mu \phi +\delta \partial _\mu \phi $$ 取代文字
    $$\delta S=\delta \int \mathcal{L}[\phi ,\partial _\mu \phi ] d^4 x =\int {\partial \mathcal{L} \over \partial \phi} \delta \phi +{\partial \mathcal{L}\over \partial (\partial _\mu \phi )} \delta \partial _\mu \phi d^4 x $$ $$=\int {\partial \mathcal{L} \over \partial \phi} \delta \phi -\partial _\mu \left({\partial \mathcal{L}\over \partial (\partial _\mu \phi )} \right)\delta \phi d^4 x +\int \partial _\mu \left({\partial \mathcal{L}\over \partial (\partial _\mu \phi )} \delta \phi \right) d^4 x $$ $$=\int \left[{\partial \mathcal{L} \over \partial \phi} -\partial _\mu \left({\partial \mathcal{L}\over \partial (\partial _\mu \phi )} \right)\right]\delta \phi d^4 x + ∮_{\partial V} {\partial \mathcal{L}\over \partial (\partial _\mu \phi )} \delta \phi d^3 x $$ $$=\int \left[{\partial \mathcal{L} \over \partial \phi} -\partial _\mu \left({\partial \mathcal{L}\over \partial (\partial _\mu \phi )} \right)\right]\delta \phi d^4 x +0$$ 因為\(\delta \phi\) 是任意，所以對任何古典物理量\(\phi\) ，必須滿足Euler-Lagrange eq $${\partial \mathcal{L} \over \partial \phi} -\partial _\mu {\partial \mathcal{L}\over \partial (\partial _\mu \phi )}=0$$ 同樣的，我們可以回到連續場的例子，\(\mathcal{L}={1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2\)，滿足 $${\partial \mathcal{L} \over \partial \phi} -\partial _t {\partial \mathcal{L}\over\partial (\partial _t \phi ) }- \nabla {\partial \mathcal{L}\over \partial ( \nabla \phi ) }=0$$ 可以迅速得到 $$-\rho\partial _t^2 \eta +Y \nabla ^2 \eta =0\to \nabla ^2 \eta ={1\over v^2} \partial _t^2 \eta $$ 如果我們將純量場\phi 推廣成向量場，例如4-displacement \(x^\nu\) 、4-potential \(A^\nu\) ，剛剛的變分只需將\(\phi\) 改寫成\(A^\nu\) ，即可得 $${\partial \mathcal{L}\over \partial x^\nu}-{d\over d\tau} {\partial \mathcal{L}\over (\partial U^\nu )}=0:Lorentz-force$$ $${\partial \mathcal{L}\over \partial A^\nu }-\partial _\mu {\partial \mathcal{L}\over\partial (\partial _\mu A^\nu ) }=0:Field-equation$$ 回到電磁場的Action $$S=S_P+S_{PF}+S_F$$ $$=-\int P_\mu U^\mu d\tau -\int {e\over c} A_\mu U^\mu d\tau -\int {1 \over 16 \pi c} F_{\mu \nu} F^{\mu \nu} d^4 x $$ $$=\int -\rho_m c-{1 \over c^2} A_\mu J^\mu -{1 \over 16 \pi c} F_{\mu \nu} F^{\mu \nu} d^4 x $$ 先計算Lorentz force $${\partial \mathcal{L}\over \partial x^\nu}-{d\over d\tau} {\partial \mathcal{L}\over (\partial U^\nu )}=0$$ 跟\(x^\nu\)有關的只有\(S_P\) 、\(S_{PF}\)，所以處理 $$\mathcal{L}=-P_\mu U^\mu -{e\over c} A_\mu U^\mu $$ $${\partial \left(-{e\over c} A_\mu U^\mu \right)\over \partial x^\nu }-{d\over d\tau} {\partial \left(-P_\mu U^\mu -{e\over c} A_\mu U^\mu \right) \over \partial U^\nu }=0$$ $$\to -{e\over c} U^\mu (\partial _\nu A_\mu )-{d\over d\tau} \left(-P_\nu-{e\over c} A_\nu \right)=0$$ $$\to-{e\over c} U^\mu (\partial _\nu A_\mu )+{dP_\nu \over d\tau } +{e\over c} {dA_\nu \over d\tau } =0$$ $$\to -{e\over c} U^\mu (\partial _\nu A_\mu )+{dP_\nu \over d\tau } +{e\over c} {\partial A_\nu \over \partial x^\mu } {dx^\mu \over d\tau} =0$$ $$\to -{e\over c} U^\mu (\partial _\nu A_\mu )+{dP_\nu \over d\tau } +{e\over c} U^\mu (\partial _\mu A_\nu )=0$$ $$\to {dP_\nu \over d\tau } +{e\over c} U^\mu (\partial _\mu A_\nu -\partial _\nu A_\mu )=0$$ $$\to {dP_\nu \over d\tau } +{e\over c} U^\mu F_{\mu\nu}=0$$ $$\to {dP_\mu \over d\tau } =-{e\over c} U^\nu F_{\nu\mu} $$ $$\to {dP_\mu \over d\tau } ={e\over c} F_{\mu \nu} U^\nu$$ 迅速得到Lorentz force。
    再來處理Field equation， $$\partial ^\mu {\partial \mathcal{L}\over \partial (\partial ^\mu A^\nu ) }-{\partial \mathcal{L} \over \partial A^\nu }=0$$ $$\partial ^\mu \left[-{1 \over 8 \pi c} F_{\alpha\beta} {\partial F^{\alpha\beta}\over \partial (\partial ^\mu A^\nu) } \right]+{1 \over c^2} J_\nu=0$$ 因為 $${\partial F^{\alpha\beta} \over \partial (\partial ^\mu A^\nu )} ={\partial (\partial ^\alpha A^\beta -\partial ^\beta A^\alpha ) \over \partial (\partial ^\mu A^\nu )}= \delta ^\alpha _\mu \delta ^\beta _\nu- \delta ^\beta _\mu \delta ^\alpha _\nu$$ $$\partial ^\mu \left[-{1 \over 8 \pi c} F_{\alpha\beta} ( \delta ^\alpha _\mu \delta ^\beta _\nu- \delta ^\beta _\mu \delta ^\alpha _\nu )\right]+{1 \over c^2} J_\nu=0$$ $$\partial ^\mu \left[-{1 \over 8 \pi c} F_{\mu\nu}+{1 \over 8 \pi c} F_{\nu\mu} \right]+{1 \over c^2} J_\nu=0$$ 因為\(-F_{\mu\nu}=F_{\nu\mu} \) $$\partial ^\mu \left[{1 \over 4 \pi c} F_{\nu\mu} \right]+{1 \over c^2} J_\nu=0$$ $$\partial _\nu F^{\mu \nu} =-{4\pi \over c} J^\mu $$

  13. 場論中的Lagrangian density不唯一性

    14. 前面提到，當Lagrangian添加一個函數\(f=f(q,t)\)時間的全微分項df/dt，並不會改變EoM。在場論中也有對應的推廣，\(\mathcal{L}\to \bar{\mathcal{L}} =\mathcal{L}+\partial _\mu f^\mu\) ，一樣要注意的是\(f^\mu =f^\mu (\phi ,x^\mu )\)只能是\((\phi ,x^\mu )\)的函數。一樣可以從兩個部分來看。第一種是最簡單的從變分的邊界， $$\delta S=\delta \int (\mathcal{L}+\partial _\mu f^\mu ) d^4 x =\delta \left[\int \mathcal{L}d^4 x +\int \partial _\mu f^\mu d^4 x \right]$$ $$=\delta \int _a^b \mathcal{L}dt+\delta ∮ f^\mu d^3 S_\mu =\delta \int _a^b \mathcal{L}dt$$ 其中\(\int \partial _\mu f^\mu d^4 x =∮ f^\mu d^3 S_\mu \)利用高斯定理，\(\delta ∮ f^\mu d^3 S_\mu =0\)來自於變分邊界不變。 另外一種是直接展開，觀察\(\mathcal{L}+\partial _\mu f^\mu\) 是否滿足 $${\partial (\mathcal{L}+\partial _\mu f^\mu )\over\partial \phi} -\partial _\mu {\partial (\mathcal{L}+\partial _\mu f^\mu )\over\partial (\partial _\mu \phi ) }=0$$
    $${\partial (\mathcal{L}+\partial _\mu f^\mu )\over\partial \phi} -\partial _\mu {\partial (\mathcal{L}+\partial _\mu f^\mu )\over\partial (\partial _\mu \phi ) }= {\partial\mathcal{L}\over\partial \phi} -\partial _\mu {\partial L\over\partial (\partial _\mu \phi ) }+{\partial (\partial _\mu f^\mu )\over\partial \phi }-\partial _\mu {\partial (\partial _\mu f^\mu )\over\partial (\partial _\mu \phi ) }$$ $$={\partial (\partial _\mu f^\mu )\over\partial \phi }-\partial _\mu {\partial (\partial _\mu f^\mu )\over\partial (\partial _\mu \phi ) }$$ 利用 $$df^\mu ={\partial f^\mu \over\partial \phi }\Big|_{x^\mu } d\phi +{\partial f^\mu \over \partial x^\nu }\Big|_\phi dx^\nu $$ $$\to \partial _\mu f^\mu ={\partial f^\mu \over\partial \phi }\Big|_{x^\mu } \partial _\mu \phi +{\partial f^\mu \over\partial x^\mu } \Big|_\phi $$ 進一步偏微分 $${\partial (\partial _\mu f^\mu )\over\partial (\partial _\mu \phi )} ={\partial f^\mu \over\partial \phi }\Big|_{x^\mu } \color{red}{ dot-cancelation-analogy}$$ 另外 $${\partial (\partial _\mu f^\mu )\over\partial \phi }\Big|_{x^\mu}={ \partial \over\partial \phi }\Big|_{x^\mu} \left({\partial f^\mu \over\partial \phi }\Big|_{x^\mu } \partial _\mu \phi + {\partial f^\mu \over\partial x^\mu }\Big|_\phi\right) $$ $$={ \partial \over\partial \phi }\Big|_{x^\mu} \left({\partial f^\mu \over\partial \phi }\Big|_{x^\mu } \right)\partial _\mu \phi +{\partial \over\partial \phi}\Big|_{x^\mu }\left( {\partial f^\mu \over\partial x^\mu }\Big|_\phi \right)$$ $$={ \partial \over\partial \phi }\Big|_{x^\mu } {\partial f^\mu \over\partial \phi }\Big|_{x^\mu } \partial _\mu \phi +{ \partial \over\partial x^\mu }\Big|_\phi { \partial f^\mu \over\partial \phi} \Big|_{x^\mu } $$ $$=\partial _\mu \left( {\partial f^\mu \over\partial \phi} \right)\to \partial _\mu and {\partial\over\partial \phi} commute$$ 所以 $${\partial (\partial _\mu f^\mu )\over\partial \phi} -\partial _\mu \left({\partial (\partial _\mu f^\mu )\over\partial (\partial _\mu \phi ) }\right)=\partial _\mu {\partial f^\mu \over\partial \phi} -\partial _\mu {\partial f^\mu \over\partial \phi} =0 $$ 故 $${\partial (\mathcal{L}+\partial _\mu f^\mu )\over\partial \phi }-\partial _\mu \left({ (\partial (L+\partial _\mu f^\mu )\over\partial (\partial _\mu \phi )}\right)={\partial \mathcal{L}\over\partial \phi} -\partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi ) }\right)=0$$ 添加\(\partial _\mu f^\mu \)不會改變EoM。

  14. 不破壞EoM的其他可能

    15. 本節為筆者推論，還不確定是否正確
    前面提到，當Lagrangian添加一個函數\(f=f(q,t)\)時間的全微分項\({df\over dt}\)，並不會改變EoM。在場論中也有對應的推廣，\(\mathcal{L}\to \bar{\mathcal{L}} =\mathcal{L}+\partial _\mu f^\mu\) ，一樣要注意的是\(f^\mu =f^\mu (\phi ,x^\mu )\)只能是\((\phi ,x^\mu )\)的函數。在此我們討論看看怎麼樣的\(f=f(q,\dot{q} ,t)\)和\(f^\mu =f^\mu (\phi ,\partial _\mu \phi ,x^\mu )\)有可能不改變EoM。原則上我們要求 $$ {\partial \dot{f} \over\partial q}-{d\over dt} {\partial \dot{f} \over \partial \dot{q} } =0$$ $${\partial (\partial _\alpha f^\alpha )\over\partial \phi} -\partial _\mu \left({\partial (\partial _\alpha f^\alpha )\over\partial (\partial _\mu \phi )}\right )=0)$$ Extended dot cancellation for \(f=f(q,\dot{q} ,t)\) type $${\partial \dot{f} \over \partial \dot{q} } ={d\over dt} {\partial f\over\partial \dot{q} }+{\partial f\over\partial q}$$ $$ {\partial \dot{f} \over\partial q}-{d\over dt} {\partial \dot{f} \over \partial \dot{q} } =0$$ $$\to {d\over dt} {\partial f\over\partial q}-{d\over dt} \left({d\over dt} {\partial f\over\partial \dot{q} }+{\partial f\over\partial q}\right)=0$$ $$\to {d^2\over dt^2} {\partial f\over\partial \dot{q} }=0$$ $$\to f=(at+b) \dot{q} +g(q,t)$$


    $${\partial (\partial _\alpha f^\alpha ) \over \partial (\partial _\mu \phi )} =\partial _\alpha {\partial f^\alpha\over\partial (\partial _\mu \phi )} +{\partial f^\mu \over\partial \phi }$$ $${\partial (\partial _\alpha f^\alpha )\over\partial \phi} -\partial _\mu \left({\partial (\partial _\alpha f^\alpha )\over\partial (\partial _\mu \phi )}\right )=0$$ $$\partial _\alpha {\partial f^\alpha\over\partial \phi} -\partial _\mu \left(\partial _\alpha {\partial f^\alpha\over\partial (\partial _\mu \phi )} +{\partial f^\mu \over\partial \phi }\right)=0$$ $$\partial _\mu \partial _\alpha {\partial f^\alpha\over\partial (\partial _\mu \phi )} =0$$ $$\partial _\mu \partial _\alpha {\partial f^\alpha\over\partial (\partial _\mu A^\gamma )} =0$$

  15. 場論中的諾特定理Noether theorem-Field theory

    16. 提到變分法就一定要與諾特定理做搭配。諾特定理表明如果系統中Lagrangian的物理量\(\phi\) 存在連續變\(\phi \to \phi +\delta \alpha\)，使得\(\mathcal{L}\to \mathcal{L}+{\delta \mathcal{L}\over\delta \alpha}\)，卻保持對稱性（不變性）\(\delta S=0\)，那麼就存在一個守恆流與之對應。這可以應用到：
    $$時間平移不變\leftrightarrow 能量守恆$$ $$空間平移不變\leftrightarrow 動量守恆$$ 廣義的證明如下，給定Lagrangian dendity \(\mathcal{L}[\phi (x^\alpha ),\partial _\mu \phi (x^\alpha ),x^\mu ]\)，之前的變分法是針對物理量\(\phi \) 做變分，現在我們同時針對物理量\(\phi\) 和時空\(x^\mu\) 變分 $$x^\mu \to \bar{x} ^\mu =x^\mu +\delta x^\mu $$ $$\phi \to \bar{\phi}=\phi +\delta \phi $$ 但是\(\phi =\phi (x^\alpha )\)是時空的函數，經過物理量\(\phi\) 和時空\(x^\mu \)同時變分後，包含自身的變分和受到時空變分的影響\(\phi (x^\alpha )\to \bar{\phi} ( \bar{x} ^\alpha )\)，令\(\bar{\phi} ( \bar{x} ^\alpha )\equiv \phi (x^\alpha )+\Delta\phi \)， $$\Delta\phi =\bar{\phi} ( \bar{x} ^\alpha )-\phi (x^\alpha )$$ $$=\bar{\phi} ( \bar{x} ^\alpha )-\phi ( \bar{x} ^\alpha )+\phi ( \bar{x} ^\alpha )-\phi (x^\alpha )$$ $$=\delta \phi +{\partial \phi \over \partial x^\alpha } \delta x^\alpha$$ 諾特定理探討變分後Action的差別： $$\delta S=\delta \int \mathcal{L}[\phi (x^\alpha ),\partial _\mu \phi (x^\alpha ),x^\mu ] d^4 x $$ $$=\int \mathcal{L}[\bar{\phi} ( \bar{x} ^\alpha ),\partial _\bar{\mu} \bar{\phi} ( \bar{x} ^\alpha ), \bar{x} ^\mu ] d^4 \bar{x} -\int \mathcal{L}[\phi (x^\alpha ),\partial _\mu \phi (x^\alpha ),x^\mu ] d^4 x $$ 很明顯可以發現到連積分的4-volune \(d^4 \bar{x}\)都發生變化。可以用乘法的微分來思考 $$\delta S=\delta \int \mathcal{L}d^4 x =\int \delta\mathcal{L} d ^4 x +\int \mathcal{L}\delta d^4 x $$ 第一項\(\delta \mathcal{L}\)在處理時要非常小心 $$\delta \mathcal{L}=\mathcal{L}[\bar{\phi} ( \bar{x} ^\alpha ),\partial _\bar{\mu} \bar{\phi} ( \bar{x} ^\alpha ), \bar{x} ^\mu ]-\mathcal{L}[\phi (x^\alpha ),\partial _\mu \phi (x^\alpha ),x^\mu ]$$ $$=\mathcal{L}[\bar{\phi} ( \bar{x} ^\alpha ),\partial _\bar{\mu} \bar{\phi} ( \bar{x} ^\alpha ), \bar{x} ^\mu ]-\mathcal{L}[\phi ( \bar{x} ^\alpha ),\partial _\bar{\mu} \phi ( \bar{x} ^\alpha ), \bar{x} ^\mu ]+\mathcal{L}[\phi ( \bar{x} ^\alpha ),\partial _\bar{\mu} \phi ( \bar{x} ^\alpha ), \bar{x} ^\mu ]-\mathcal{L}[\phi (x^\alpha ),\partial _\mu \phi (x^\alpha ),x^\mu ]$$ $$={\mathcal{L}[\phi +\delta \phi ,\partial _\bar{\mu} \phi +\delta (\partial _\bar{\mu} \phi ), \bar{x} ^\mu ]-L[\phi ,\partial _\bar{\mu} \phi , \bar{x} ^\mu ]}+{\mathcal{L}[\phi ,\partial _\bar{\mu} \phi , \bar{x} ^\mu ]-L[\phi ,\partial _\mu \phi ,x^\mu ]}$$ $$={{\partial \mathcal{L}\over\partial \phi} \delta \phi +{\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \delta (\partial _\mu \phi )}+{{\partial \mathcal{L}\over \partial x^\mu } \delta x^\mu }$$ 利用\(\partial _\mu \)拉到前面去 $$={{\partial \mathcal{L}\over\partial \phi} \delta \phi -\partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \right)\delta \phi +\partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \delta \phi \right)}+{{\partial \mathcal{L}\over \partial x^\mu } \delta x^\mu }$$ 可以注意到\(\left[{\partial \mathcal{L}\over\partial \phi} -\partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \right)\right]\delta \phi\) 是Euler-Lagrange eq等於零。所以 $$\delta \mathcal{L}=\partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \delta \phi \right)+\partial _\mu \mathcal{L}*\delta x^\mu $$ 第二項\(\delta d^4 x\)要用到Jacobian $$\int \mathcal{L}\delta d^4 x =\int \mathcal{L}d^4 \bar{x} -\int \mathcal{L}d^4 x $$ $$d^4 \bar{x}=J\left({\partial \bar{x} ^\mu \over\partial x^\nu }\right) d^4 x$$ \(J\left({\partial \bar{x} ^\mu \over\partial x^\nu }\right)\)為Jacobian determinant $${\partial \bar{x} ^\mu \over\partial x^\nu }={\partial (x^\mu +\delta x^\mu )\over\partial x^\nu }= \delta ^\mu _\nu +\partial _\nu \delta x^\mu $$ Jacobian determinant計算出來為 $$J\left({\partial \bar{x} ^\mu \over\partial x^\nu }\right)=1+\partial _\mu \delta x^\mu $$ 所以 $$\int \mathcal{L}\delta d^4 x =\int \mathcal{L}*\partial _\mu \delta x^\mu d^4 x $$ 合併兩項 $$\delta S=\delta \int \mathcal{L}d^4 x =\int \left[\partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \delta \phi \right)+\partial _\mu L*\delta x^\mu \right] d^4 x +\int \left[\mathcal{L} *\partial _\mu \delta x^\mu \right] d^4 x $$ $$=\int \partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \delta \phi \right)+\partial _\mu \mathcal{L}*\delta x^\mu +\mathcal{L} *\partial _\mu \delta x^\mu d^4 x $$ $$=\int \partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \delta \phi \right)+\partial _\mu (\mathcal{L}\delta x^\mu ) d^4 x $$ $$=\int \partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \delta \phi +\mathcal{L}\delta x^\mu \right) d^4 x =0$$ 其中\(\delta \phi \)是\(\phi\) 自身的變分，不包含受到\(\delta x^\mu\) 的影響，我們想要考慮廣義一點，改寫成\(\Delta\phi \)可以包含受到\(\delta x^\mu \)的影響。因為\(\Delta\phi =\delta \phi +\partial _\alpha \phi *\delta x^\alpha\)，所以 $$\delta S=\int \partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} (\Delta\phi -\partial _\alpha \phi *\delta x^\alpha )+\mathcal{L}\delta x^\mu \right) d^4 x $$ $$=\int \partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \Delta\phi -\left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \partial _\alpha \phi - \delta ^\mu _\alpha \mathcal{L}\right)\delta x^\alpha \right) d^4 x$$ 令 $$\left(\begin{matrix} \delta x^\alpha \\ \Delta\phi \end{matrix}\right)=\varepsilon\left(\begin{matrix} Χ^\alpha \\ \Psi \end{matrix}\right)$$ \(Χ^\alpha\)、\(\Psi\)為Symmetry generators， $$\delta S=\varepsilon \int \partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \Psi-\left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \partial _\alpha \phi - \delta ^\mu _\alpha L\right) Χ^\alpha \right) d^4 x =0$$ 因為\(\varepsilon \)是任意的，所以 $$\partial _\mu \left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \Psi-\left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \partial _\alpha \phi - \delta ^\mu _\alpha \mathcal{L}\right) Χ^\alpha \right)\equiv \partial _\mu N^\mu =0$$ 定義諾特流(Noether current) $$N^\mu \equiv {\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \Psi-\left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \partial _\alpha \phi - \delta ^\mu _\alpha \mathcal{L}\right) Χ^\alpha $$ 其中，\({\partial \mathcal{L}\over\partial (\partial _\mu \phi )}\) 是對應到物理量\(\phi \)在對稱變換\(\Psi\)的守恆流，\(\left({\partial \mathcal{L}\over\partial (\partial _\mu \phi )} \partial _\alpha \phi - \delta ^\mu _\alpha \mathcal{L}\right)\)是對應時空\(x^\mu\) 變化\(Χ^\alpha\)下的守恆流。

    如果是向量場\(\alpha^\nu\)， $$N^\mu \equiv {\partial \mathcal{L}\over\partial (\partial _\mu \alpha^\nu )} \Psi^\nu-\left({\partial \mathcal{L}\over\partial (\partial _\mu \alpha^\nu )} \partial _\alpha \alpha^\nu- \delta ^\mu _\alpha \mathcal{L}\right) Χ^\alpha $$

  16. 諾特定理與對稱性-時空與能量動量守恆

    17. 在討論時空對稱性時，我們固定物理量\(\phi \)不受變分影響，\(\Psi=0\)時，只剩下 $$\partial _\mu \left[\left({\partial \mathcal{L}\over\partial \left(\partial _\mu \phi\right) } \partial _\alpha \phi - \delta ^\mu _\alpha L \right) Χ^\alpha \right]=0$$ 我們定義能量動量張量Energy momentum tensor \(T^{\mu\nu}\) $$T^{\mu\nu}\equiv {{\partial L}\over{\partial \left( \partial _\nu \phi \right)}} \partial ^\mu \phi -\eta ^{\mu\nu} L$$ 守恆流\(\partial _\nu T^{\mu\nu}=0\)分別代表 $$\partial _\nu T^{0\nu}=0能量守恆$$ $$\partial _\nu T^{i\nu}=0動量守恆$$ 在相對論中，一個自由粒子的能量動量張量為 $$T^{\mu\nu}\equiv mU^\mu U^\nu$$ 其中 對古典粒子來說，回到非相對論性的話，粒子的軌跡\(q\)只與\(t\)有關， $$T^{\mu\nu}=T^{00}={\partial L\over \partial \dot{q} } \dot{q} -L=H$$ \(T^{00}\)就是Hamiltonian，能量守恆律 $$\partial _\nu T^{0\nu}=\partial _0 T^{00}={dH \over dt}=0$$ 能量不隨時間改變！
    古典的諾特定理表述為

    $$古典非相對論性$$$$相對論性$$
    $$S=\int Ldt $$$$S=\int \mathcal{L}d^4 x$$
    $$N\equiv {\partial L\over\partial \dot{q} _i } Q_i-\left({\partial L\over\partial \dot{q} _i } \dot{q} _i-L\right)T$$ $$N^\mu \equiv {\partial \mathcal{L}\over\partial (\partial _\mu \alpha^\nu ) } \Psi^\nu-\left({\partial \mathcal{L}\over\partial (\partial _\mu \alpha^\nu ) } \partial _\alpha \alpha^\nu- \delta ^\mu _\alpha L\right) Χ^\alpha $$
    古典中，時間\(t\)佔的角色對應於時空\(x^\mu\) ，所以時間的對稱性代表能量守恆，其餘的對稱性\(Q_i\)可是空間\(q_i\)、角度\(\theta_i\)，分別是 $${\partial L\over\partial \dot{q} _i } 動量守恆$$ $${\partial L\over \partial \dot{\theta}_i } 角動量守恆$$

  17. 邁向廣義相對論

    18. 古典場論的大基礎：電磁學和廣義相對論。古典電磁學因為線性的特性，常作為許多物理理論的試驗典範，常利用電磁學作為相對論性最小作用原理的示範基礎，量子化的量子場論也率先由量子電動力學打頭陣。

    另一方面，廣義相對論透過等效性原理與廣義化的相對性原理，成功將重力效應整合進時空的曲率中，將時空的物理實在性提供了新的見解。同樣的，愛因斯坦場方程式也可以透過希爾伯特-愛因斯坦作用量 (Hilbert-Einstein action) 變分推得。

    希爾伯特-愛因斯坦作用量由希爾伯特在 1915 年，幾乎與愛因斯坦同時得到愛因斯坦場方程式。廣義相對論核心的數學模型為（偽）黎曼幾何（pseudo-Riemann geometry），簡單來說利用流形 (manifold) 的切叢 (Tangent bundle) 上給予逐點可變的度規 \(g_{\mu\nu}\)（metric），賦予其相異於平直的歐式空間新的結構，屬於非歐幾何重要的一個分支。

    希爾伯特-愛因斯坦作用量寫為： \[ S = \int \mathcal{L} \sqrt{-g} \, d^4x = \frac{c^4}{16\pi G} \int R \sqrt{-g} \, d^4x + \int \mathcal{L}_M \sqrt{-g} \, d^4x \] 其中： \[ \mathcal{L} = \left( \frac{c^4}{16\pi G} R + \mathcal{L}_M \right) \sqrt{-g} = \left( \frac{1}{2\kappa} R + \mathcal{L}_M \right) \sqrt{-g} \] \(R = g^{\mu\nu} R_{\mu\nu} = g^{\mu\nu} \delta^\beta_\alpha R^\alpha_{\mu\beta\nu}\) 是 Ricci scalar，\(R_{\mu\nu}\) 是 Ricci curvature tensor，\(R^\alpha_{\mu\beta\nu}\) 是 Riemann curvature tensor（黎曼曲率張量），\(g = \det(g_{\mu\nu})\)，\(\mathcal{L}_M\) 是物質的 Lagrangian density。

    曲率張量 \(R^\alpha_{\mu\beta\nu}\) 定義如下： \[ R^\rho_{\sigma\mu\nu} = \partial_\mu \Gamma^\rho_{\nu\sigma} - \partial_\nu \Gamma^\rho_{\mu\sigma} + \Gamma^\rho_{\mu\lambda} \Gamma^\lambda_{\nu\sigma} - \Gamma^\rho_{\nu\lambda} \Gamma^\lambda_{\mu\sigma} \] 其中 \(\Gamma^\rho_{\nu\sigma}\) 是切叢聯絡（Tangent connection），在基礎的廣義相對論教科書中稱為 Christoffel symbol，可以簡單理解為非平直座標係下不同點基底向量的變化。

    有趣的是，切叢聯絡 \(\Gamma^\rho_{\nu\sigma}\) 與曲率張量 \(R^\alpha_{\mu\beta\nu}\) 在數學語言中，地位與電磁場的 \(A_\sigma\)、\(F_{\beta\mu}\) 相同。事實上，只要把切叢聯絡 \(\Gamma^\rho_{\nu\sigma}\) 與曲率張量 \(R^\alpha_{\mu\beta\nu}\) 的前兩個指標「藏起來」，可以得到： \[ \Gamma^\rho_{\nu\sigma} = \left(\Gamma^\rho_\nu \right)_\sigma = \mathbf{\Gamma}_\sigma \leftrightarrow A_\sigma \] \[ R^\alpha_{\mu\beta\nu} = \left(R^\alpha_\mu \right)_{\beta\nu} = \mathbf{R}_{\beta\nu} \leftrightarrow F_{\beta\nu} \]

    前兩個指標實際上不是向量指標，而是「李代數（Lie algebra）指標」。讀者們如果有機會學習規範理論（或稱為 Yang-Mills Theory），可以進一步理解如何將電磁作用 \(U(1)\)、弱交互作用 \(SU(2)\)、強交互作用 \(SU(3)\) 整合為主叢聯絡（Principal connection）。

    事實上，可以深入比較廣義相對論和規範理論的相似之處，或參考諾貝爾獎得主楊振寧的著名論文 10.1103/PhysRevD.12.3845、科普文章「楊振寧與當代數學」、或 Singer 在「The Mathematical Heritage of Hermann Weyl (1988, American Mathematical Society)」的文章。

  18. 淺談希爾伯特變分

    19. 在傳統廣義相對論的框架下，\(\Gamma^\rho_{\nu\sigma}\) 聯絡採用「度規相容（metric compatible）」與「無撓率（torsion-free）」的假設。前者「度規相容（metric compatible）」大意是說度規沿著 \(\Gamma^\rho_{\nu\sigma}\) 聯絡做「平行移動（parallel transport）」的時候不變： \[ \nabla_\beta g_{\mu\nu} = g_{\mu\nu;\gamma} = g_{\mu\nu,\gamma} - g_{\alpha\nu} \Gamma^\alpha_{\mu\gamma} - g_{\alpha\mu} \Gamma^\alpha_{\nu\gamma} = 0 \] 白話來說，就是物體的長度從 A 點平移到 B 點長度不變。

    後者「無撓率（torsion-free）」的假設則在於 \(\Gamma^\rho_{\nu\sigma}\) 聯絡的兩個下標是對稱的： \[ \Gamma^\rho_{\nu\sigma} = \Gamma^\rho_{\sigma\nu} \] 數學上有定理可以證明，給定度規分佈下，可以唯一決定無撓率的 \(\Gamma^\rho_{\nu\sigma}\) 聯絡。有興趣的讀者可以參考 Loring W. Tu 的著作 Differential Geometry: Connections, Curvature, and Characteristic Classes 中的 Theorem 6.6。

    這兩個條件可以導出聯絡與度規的關係： \[ \Gamma^\alpha_{\mu\gamma} = \frac{1}{2} g^{\alpha\nu} \left( g_{\nu\mu,\gamma} + g_{\nu\gamma,\mu} - g_{\mu\gamma,\nu} \right) \] 表明 \(\Gamma^\rho_{\nu\sigma}\) 聯絡與度規的一次微分有關，進一步可以表明 \(R^\alpha_{\mu\beta\nu}\)、\(R_{\mu\nu}\)、\(R\) 會與度規的二次微分有關。

    重力的 Lagrangian density \(L_G\) 表示為： \[ L_G = \frac{c^4}{16\pi G} R \sqrt{-g} = L_G \left( g_{\mu\nu}, g_{\mu\nu,\alpha}, g_{\mu\nu,\alpha\beta} \right) \] 希爾伯特利用對度規（metric）變分，可以得到愛因斯坦場方程式。不過在這種觀點下，\(L_G\) 會與度規的二次微分有關。

    前文提及 Ostrogradsky instability，我們預期 \(L\) 只會依賴於場的一次微分，否則會導致能量沒有下限的問題。下一節我們將利用 Palatini 變分法，將聯絡場與度規場視作獨立的場分別變分，亦可得到相同的結論。

    此時，由於聯絡場與度規場各自獨立，\(R_{\mu\nu}\) 只是聯絡的一次微分，因此 \(L_G\) 可以寫成： \[ L_G = \frac{c^4}{16\pi G} g^{\mu\nu} R_{\mu\nu} \sqrt{-g} = L_G \left( g^{\mu\nu}, \Gamma^\alpha_{\mu\gamma}, \Gamma^\alpha_{\mu\gamma,\beta} \right) \] 這樣可以安全地避免二次微分問題。

後記
感謝兩位在清華的恩師：吳國安教授 和 周定一教授。國安教授教導我大學部的理論力學、周教授教導我古典力學和廣義相對論。他們的教學熱情和用心讓我可以欣賞到古典物理之美=)


Index
Contact:
取代文字