超導量子位元(科普版)
Author:Peir-Ru Wang
\(\to\)English Version
Update
(11)2025.02.07:QPU拓墣
(10)2025.02.06:電子顯微鏡下的超導量子位元
(09)2025.02.05:其他種類的Qubit
(08)2025.02.04:超導量子電腦長什麼樣子?
(07)2025.02.03:當前主流超導量子位元的種類
(06)2025.02.02:淺談超導電路量子位元的種類
(05)2025.02.01:如何送訊號到量子位元?
(04)2025.01.24:早年超導量子位元的種類
(03)2025.01.12:超導量子位元是什麼呢?
(02)2025.01.10:約瑟夫森節
(01)2025.01.06:主題建立
- 約瑟夫森節
- 超導量子位元是什麼呢?
- 淺談超導電路量子位元的種類
- 以超導電路為基礎,採用約瑟夫森節,有時候稱為人造原子(Artificial Atom),單一Qubit尺寸為約為微米\( \left( \mu m \right) \)等級。本文討論即為此類的Qubit。
- 拓墣量子位元,採用超導體為基底,表面放置奈米線,因為鄰近效應的關係,奈米線會被底層的超導體影響成超導性。施加磁場破壞時間反演對稱性,奈米線兩端會形成特殊的Majorana State。未來會有機會討論\(^a\)。
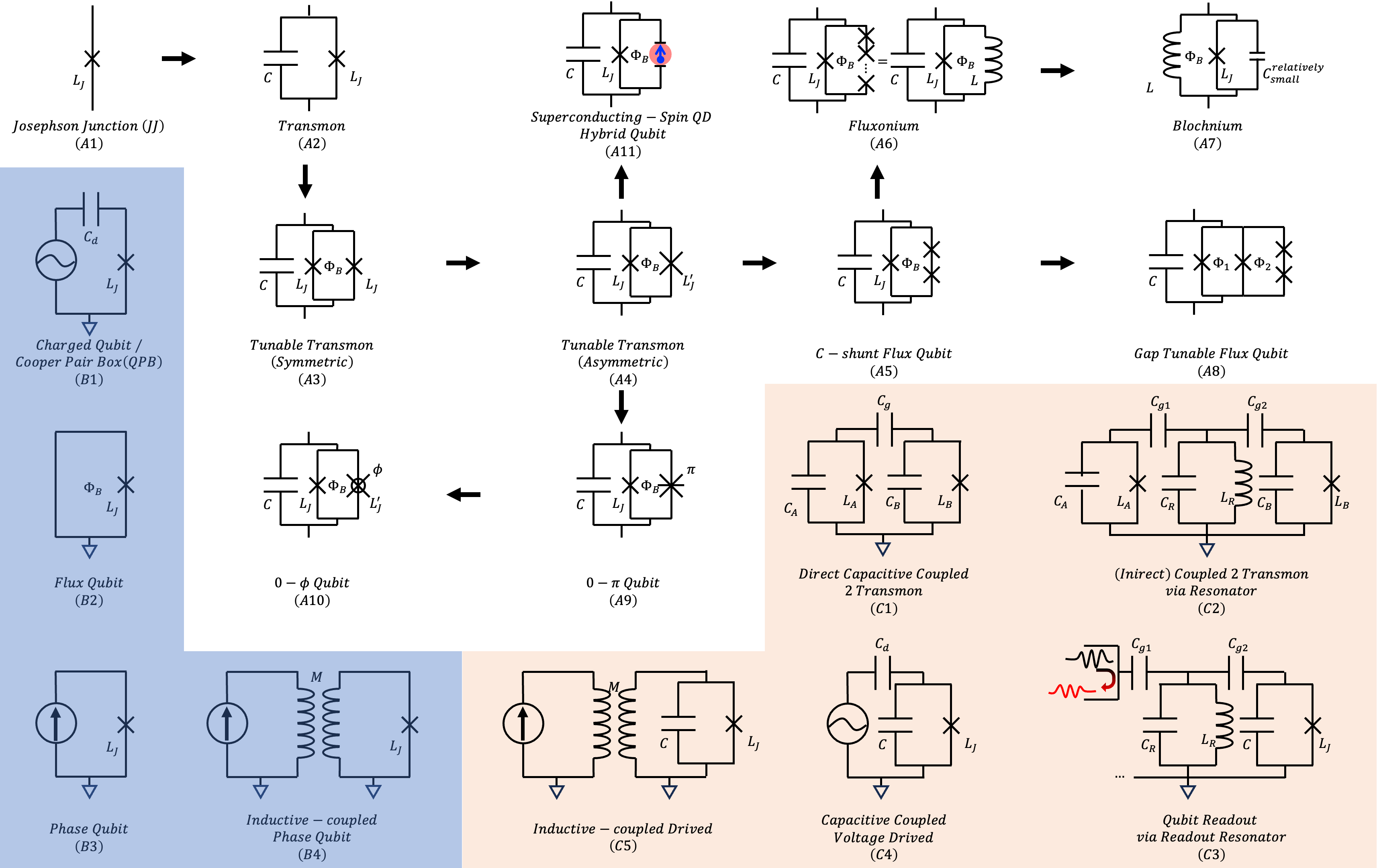
- Type A: A1,以單一約瑟夫森節JJ作為量子位元,為較早期的Qubit設計。
- Type B: A2~A8,以電容並聯(C-shunt)一個JJ為基礎。後期為了更進一步增加Qubit的相干時間,朝向並聯大電感、縮小電容,來減緩雜訊的影響。
- Type C: A9~A10,此類Qubit針對其中一側的JJ性質做變化\(^{j}\),使得其基態相位差不為0。實現的方式可以利用較複雜的電路設計\(^{a,b,c}\)、或是將絕緣層替換為磁性材料\(^{d,i}\)、或是採用s-wave搭配d-wave的異質JJ\(^{g,h}\)。
- Type Hybrid: A11,這類是以超導位元結合自旋量子點(Spin Quantum Dot, Spin QD)的複合\(^{k}\)。此外可以與超流氦形成複合Qubit\(^{e,f}\)、離子井等,可以參考\(^l\)。
- 早年超導量子位元的種類
- 當前主流超導量子位元的種類
- 電子顯微鏡下的超導量子位元
- 其他種類的Qubit
- 超導量子電腦長什麼樣子?
- 控制頻率*1:挑控磁通量的Fluxline。
- 控制狀態*1:Driveline。
- 讀取狀態*2:Readout line一進一出。
- 如何送訊號到量子位元?
- QPU拓墣
- 如何控制超導量子位元
- 脈衝的振幅(Amplitude \( A \)): 改變 Qubit 的狀態(Block sphere 的轉角)
- 脈衝的時長(Duration \( T \)): 改變 Qubit 的狀態(Block sphere 的轉角)
- 脈衝的頻率(Frequency \( \omega_d \)): 決定是否能精確驅動 Qubit
- 脈衝的包絡(Envelop \( F(t, \tau) \)): 影響漏態(Leakage)
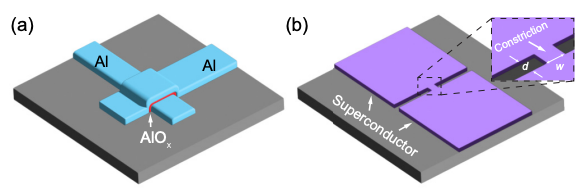
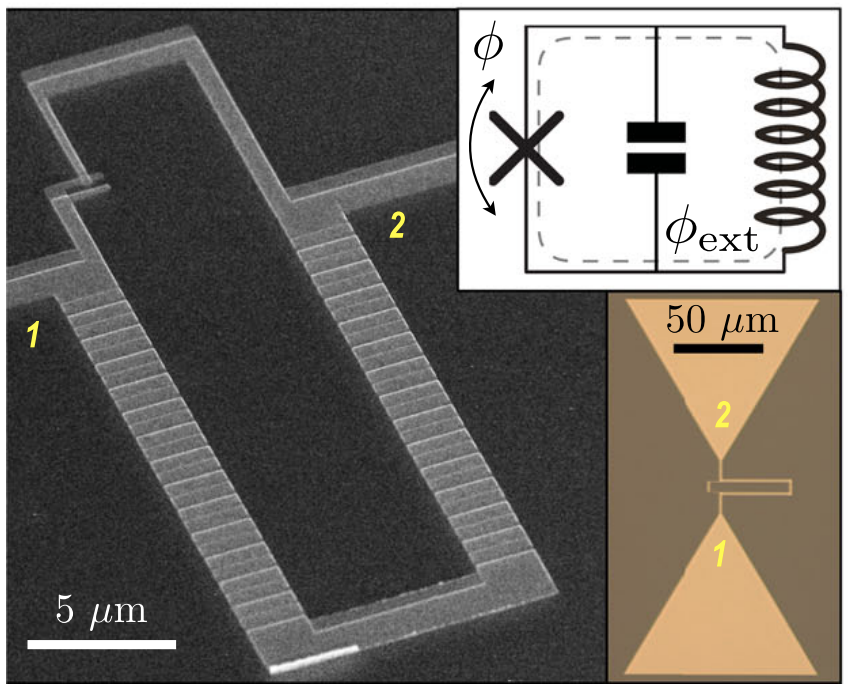
以超導製作的量子位元基本上都脫不開約瑟夫森節(Josephson Junction)。約瑟夫森節是一種三明治結構,以兩個超導體中間夾一個非超導態的物質,因為量子效應,超導電流可以透過穿隧效應穿越這層非超導層。常見製作材料為鋁基(Al)或是鈮基(Nb),在基板上鍍一層超導金屬之後,讓表面氧化形成一層薄薄的氧化層(即絕緣非超導層),再鍍上另一層超導金屬,即是一個約瑟夫森節,這種超導-絕緣-超導結構稱為SIS結(Superconductor-Insulator-Superconductor, SIS junction)。
▲(a)SIS約瑟夫森節的示意圖。(b)電子顯微鏡下的鋁基SIS節。(c)鋁的超導溫度\(T_c = 1.2K\),而鈮的擁有單元素裡面最高的超導溫度\(T_c = 9.2K\),故如果用鈮來做量子位元可以有比較高的穩定度。可是鈮的氧化物\(Nb_2O_5\)與金屬鈮結構差異過大,難以製作成性能良好的約瑟夫森節,故利用多層的材料\(Nb-Re-Al_2O_3-Al-Nb\),採用氧化鋁當絕緣層搭配薄薄的\(Re\)、\(Al\)當結構緩衝層。這種緩衝手法再現今半導體製程上也很常出現(異質整合),緩衝層大概約兩三層原子,作為橋接兩個晶格常數不匹配得材料。在量子材料中另一個很常見的量子效應-鄰近效應(Proximity effect),即塊材的波函數會完全進入到薄膜層,使得薄膜的物理性質「變成」塊材的物理性質。在這邊也會因為鈮超導的鄰近效應,使得緩衝層也變為超導性,故這個多層結構也是SIS。
Ref:10.1557/mrs.2013.229
▲Nb的約瑟夫森節例子
Ref:David Schuster of Stanford University
https://www.anl.gov/article/resurrecting-niobium-for-quantum-science
https://schusterlab.stanford.edu/research.html
▲量子效應是很脆弱的,事實上約瑟夫森節非常脆弱,要形成良好的絕緣層「並」整合在三明治結構中是非常挑戰的。如果結構中有不良的缺陷,會導致量子位元退相干、產生錯誤。故科學家也不斷的思考不同的解決方案。圖b為一種理論建議,利用收窄的效果,使局部失去超導性,即自然形成一個約瑟夫森節(ScS)。
Ref:10.1103/PhysRevA.110.012427
https://quantumzeitgeist.com/superconducting-qubits-get-boost-with-novel-constriction-design/
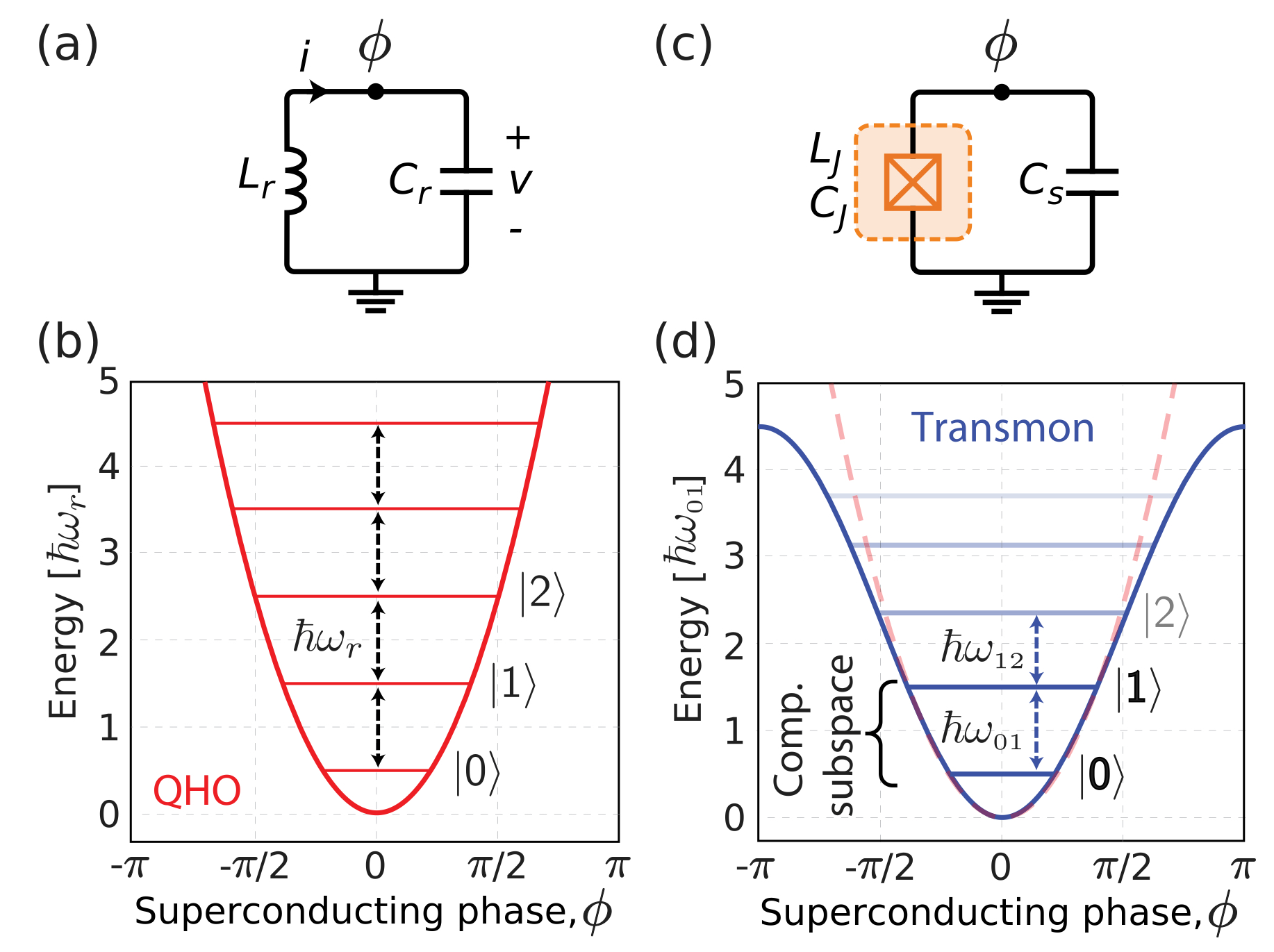
在古典計算中,一系列古典位元以0或1兩個狀態來紀錄資訊,同樣的,量子位元也是利用不同的量子狀態來記錄資訊和計算。最簡單的量子能階概念即為量子簡諧震盪(Quantum Simple Harmonic Oscillator)。想要用電子電路來實踐簡諧震盪,最簡單的方式就是一個\(LC\)電路,由一個電感\(L\)與一個電容\(C\)組成,可以見下圖(a)。古典的簡諧震盪是連續的,但在量子世界裡能階簡諧震盪是不連續的,可以利用不同能階來記錄訊息,我們習慣以\( \ket{0} \)、\(\ket{1}\)、\(\ket{2}\)...或\( \ket{g} \)、\(\ket{e}\)、\(\ket{f}\)...代表不同能量的能階,可以參考下圖(b)。可以看到圖(b)每個能階的差距是相同的,都是\(\hbar \omega_r\)。然而當我們要操作量子位元則的時侯,會希望系統被限制在\( \ket{0} \)和\(\ket{1}\)之間作轉換就好,此時就需要非線性元件來區分\( \ket{0} \)和\(\ket{1}\)與其他不想要的能階。約瑟夫森節就是良好的非線性電感元件,如圖(c)。圖(d)可以看到能階差距發生變化,就可以利用能階不圖的特性,來操作量子位元。故最基本的超導量子位元即為一個超導電容與一個約瑟夫森節組成!
Ref: 10.1063/1.5089550
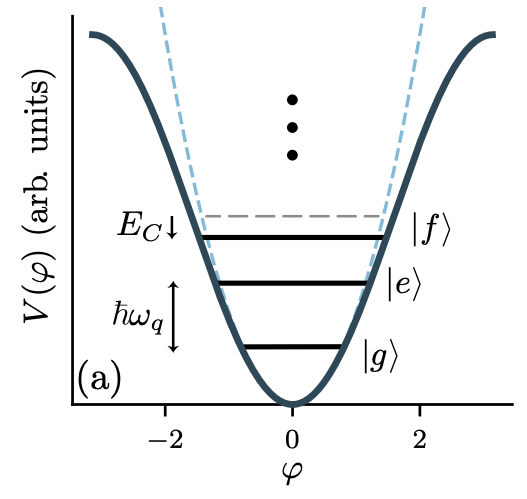
▲此圖也可以很明顯展示超導量子位元能階變化,第二激發態\(\ket{f}\)(或\(\ket{2}\))能量較低。
Ref: 10.1103/RevModPhys.93.025005
以超導為基礎的量子位元可以區分為兩大類:
以約瑟夫森節構成的超導電路,可以參考下圖呈現不同名稱的超導Qubit:
A系列表示組成一個Qubit最基本的單元,箭頭為概念的延伸方向,我自己會分為四大類:
\(^b\)10.1088/1367-2630/aab7cd
\(^c\)10.1088/1367-2630/ab09b0
\(^d\)10.1038/s43246-024-00659-1
\(^e\)10.1103/PhysRevA.101.012336
\(^f\)10.1038/s41467-019-13335-7
\(^g\)10.1109/TASC.2019.2892078
\(^h\)10.1088/1361-6668/ab7053
\(^i\)10.1103/PhysRevApplied.8.054028
\(^j\)10.1088/0953-2048/21/3/034011
\(^k\)10.1038/s41567-023-02071-x
\(^l\)arXiv: 1204.2137
(A8) https://www.ntt-review.jp/archive/ntttechnical.php?contents=ntr201209fa2.html
B系列為Type A Qubit搭配控制電路,利用不同控制電路的方式,有不同的名稱,可以參考<早年超導量子位元的種類>
。
C系列為Type B Qubit搭配控制電路的範例。
基本上所有的超導量子位元都奠基在約瑟夫森節為基礎,搭配電容和電感做組合。早年的超導量子位元可以見下圖:
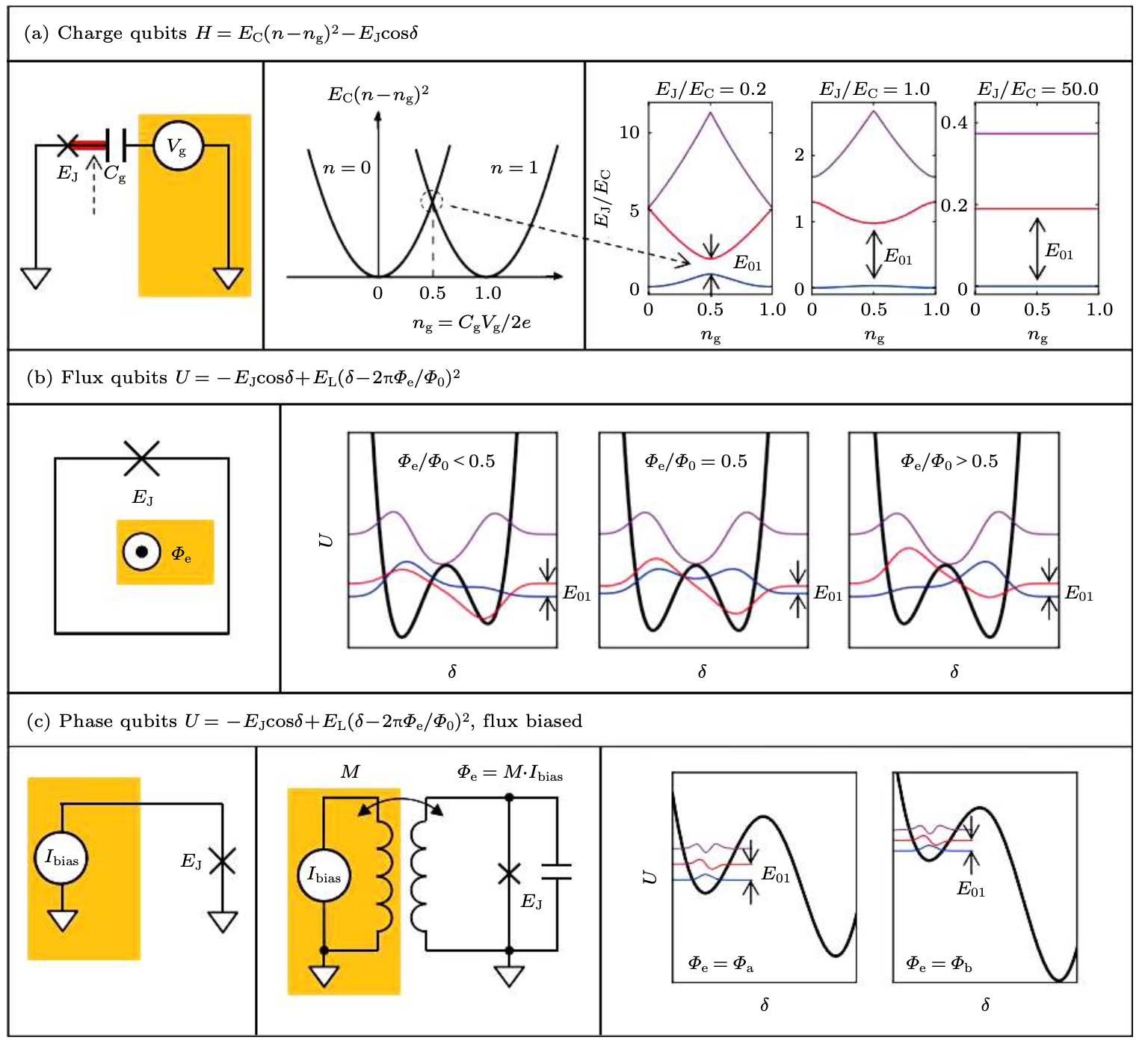
▲早期的超導量子位元分成三大類:Charge Qubit、Flux Qubit和Phase Qubit。簡易的概念差別在於主要控制Qubit的手段差異(途中黃色框框):
\(\to\)(a)用電壓控制:因為電壓可以改變電容的儲電量,故稱為Charge Qubit
\(\to\)(b)用磁通量控制:磁通量會改變約瑟夫森節的儲能,稱為Flux Qubit
\(\to\)(c)用感應電流控制:感應電流會改變約瑟夫森節的相位,稱為Phase Qubit
Ref: 10.7498/aps.71.20211865
早期的超導Qubit進一步的演化,可以參看下圖:
早期的超導Qubit容易受到雜訊的影響,需要仰賴外部控制電路來形成能階,外部控制電路常常是大型控制儀器(這裡指的「大型」是相對於微米等級的JJ,讀者可以想像就是日常電腦等級的大小,特徵尺度為公分),如此大型的積體電路就會有許多古典雜訊,會導致量子位元退相干。為了提升保真度(Fidelity),將一個電容\(C\)並聯,構成所謂的Transmon。此時一個Transmon即構成一個\(LC\)電路,有自身量子化的能階。
因為Transmon有自身的量子頻率,若要控制Transmon進行量子運算,需要精準的頻率控制與其共振來改變其量子態。當進行大型量子電路發展時,一條控制線或讀取線常會串連多個Qubit,此時如果彼此頻率太相近,會導致訊號影響到頻譜上鄰近的Qubit,是crosstalk的成因之一。調控頻率的方式需從改變電容職值\(C\)或是約瑟夫森節的電感值\(L_J\)做調整,必須從製程上進行參數調控,但要在製程中同時精準控制不同Qubit間的頻率隔離,非常的複雜。加上製成可能造成的誤差,一旦離開製程階段便無法調整,容易造成良率下降。此外,約瑟夫森節實際上會隨時間(每個月甚至每天)偏離原本預設的頻率,這是由於材料異質接面常見的物體,會因為原子移動、缺陷移動等擴散,慢慢改變接面的形狀,一旦頻率偏離過大,整個電路就會失效。故尋找可以「後天調頻」的Transmon顯現其重要性。科學家採用兩個JJ構成的SQUID來構成Tunable Transmon,透過兩個JJ之間的磁通量,可以調控Transmon的頻率。如此一來便可以在量子計算時,同步校正每個Qubit,並達到頻率隔離。構成Tunable Transmon的雙約瑟夫森節可以是相同的(對稱Symmetric)或是不同的(非對稱Asymmetric)。對稱的設計有較大的頻率可調範圍,但相對的就極異受調控磁通量的雜訊;反之對稱的設計雖然頻率可調範圍較小,但頻率的穩定度就較高。
一個Transmon雖然脫離對外部控制儀器的依賴,但因為其加入一個電容\(C\),電容是利用正負電荷分離來進行儲能,可以想像這是一個微米等級的偶極,極易受到電磁訊號的干擾導致退相干。在電路設計上,常利用電感當作濾波、抗干擾的元件,科學家便從其中一側的約瑟夫森節著手,改成串連許多約瑟夫森節構成一個電感\(L\),稱為Fluxonium。目前Fluxonium可以達到微秒等級的退相干時間。
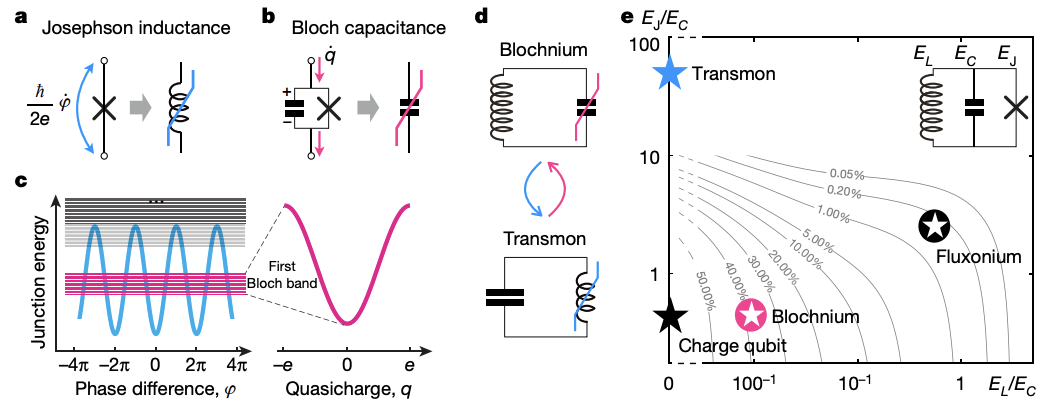
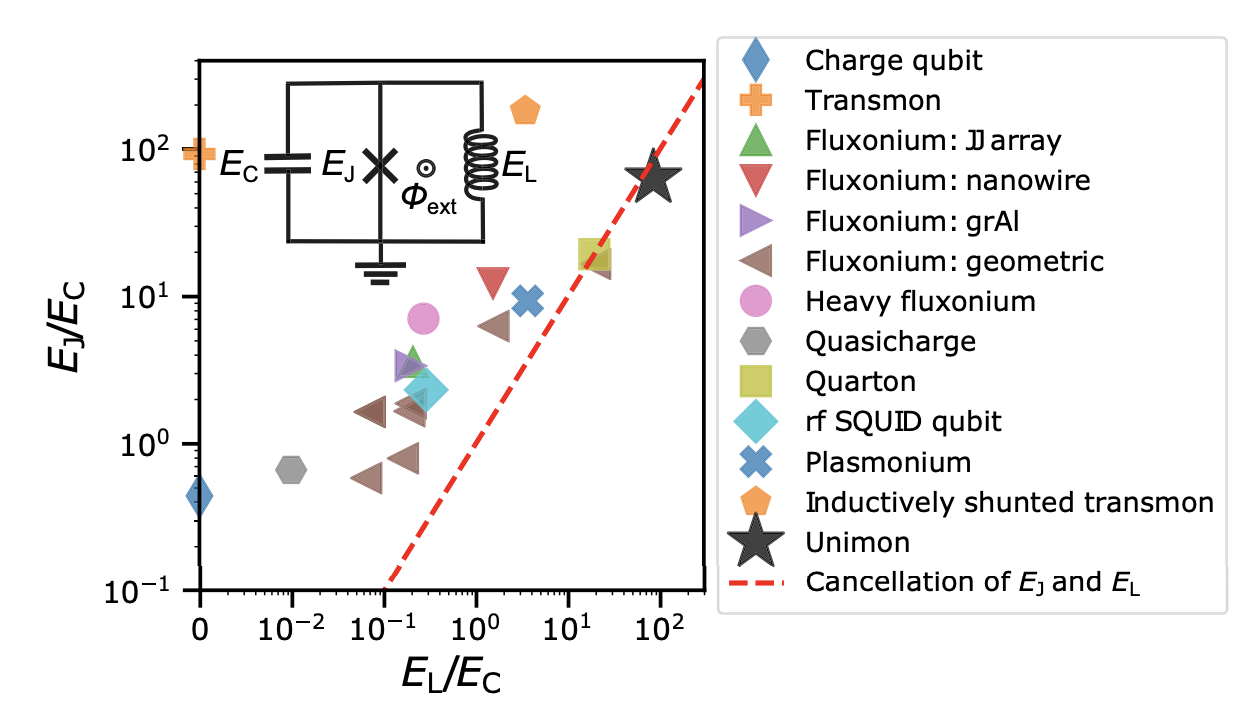
更進一步提升Qubit的穩定度,目前方向是不斷提升電感\(L\)、並減少電容\(C\),有一系列的發展稱為Blochnium。可以參考下面兩張圖,不同的超導Qubit實際上就是調整\(L\)、\(C\)和\(J\)。
▲此圖右半部說明Transmon和Blochnium概念的對偶,Transmon是「非線性電感」搭配電容,Blochnium可以看成是「非線性電容」搭配電感。
Ref: 10.1038/s41586-020-2687-9
Ref: ar5iv.labs.arxiv.org/html/1907.02937
arxiv.org/pdf/2106.11352
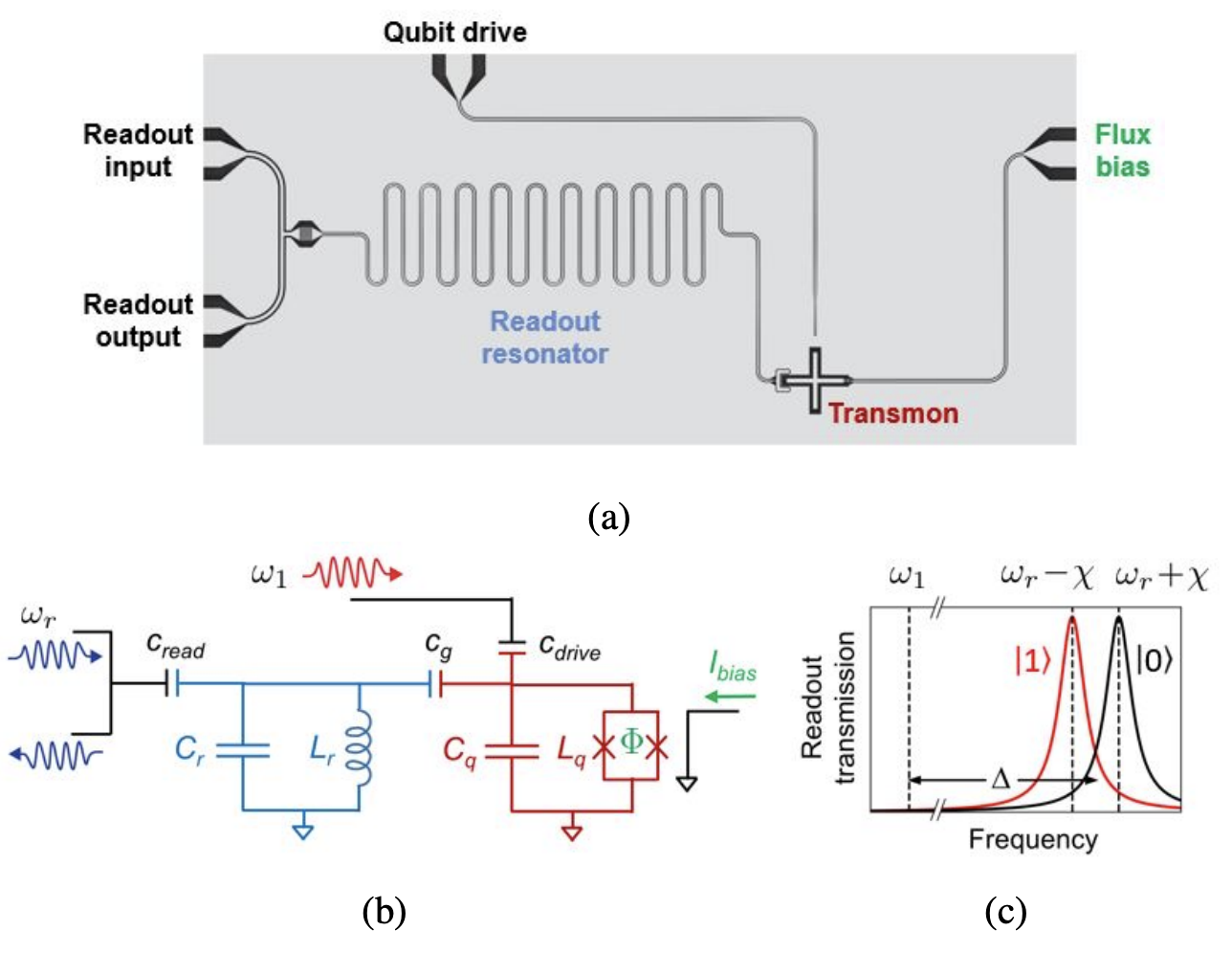
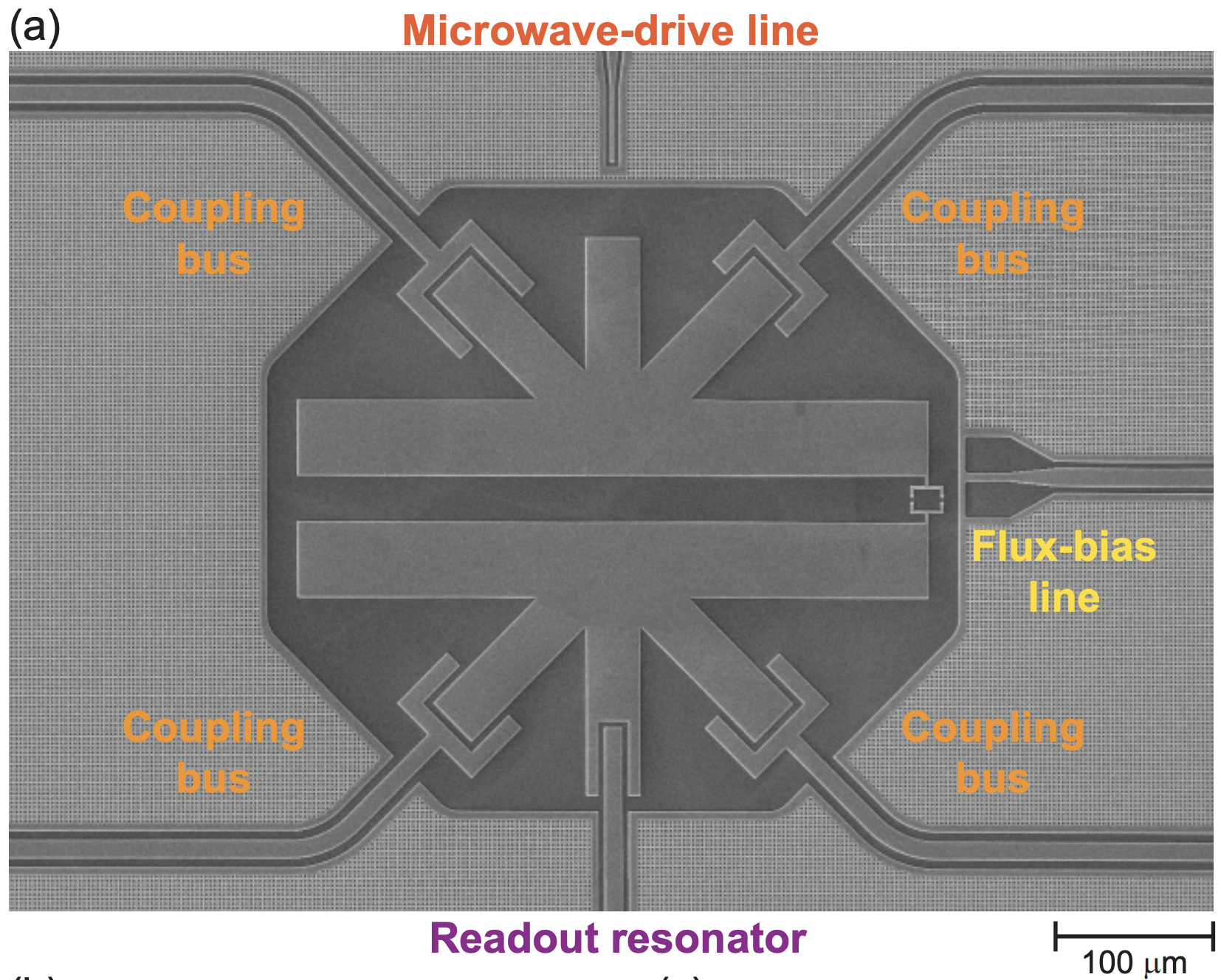
▲首先可以先欣賞一下Transmon的 layout。(a)顯微鏡底下的電路圖,(b)對應的電路圖,此圖中有一個 Qubit(紅色 Transmon)、一個 readout resonator(天藍色),兩條 feed\mathcal{L}ine 個別驅動(Drive)量子位元與 readout resonator。各元件間利用電容作耦合。另外有一條 Flux line 連到 Qubit 旁,會產生磁場來改變 Transmon 的操作頻率。(c)readout resonator 因為與量子位元耦合,會受到量子位元在 \(|0\rangle\) 或 \(|1\rangle\) 狀態的差異產生頻譜的位移,利用 readout resonator 頻譜的位移的特性來得知量子位元的狀態。
▲從其中一側的約瑟夫森節著手,改成串連許多約瑟夫森節構成一個電感\(L\),稱為Fluxonium。
Ref: 10.1038/s41467-021-26686-x
▲Blochnium可以說是電感進一步串連的Fluxonium。其立體結構非常有趣。
Ref: 10.1038/s41586-020-2687-9
▲另一張Fluxonium/Blochnium中的約瑟夫森節陣列蝕刻製程的圖片。此圖可以很明顯地看出捲鬚結構是由一連串的約瑟夫森節串連而成。
Ref: arxiv: 2411.10396
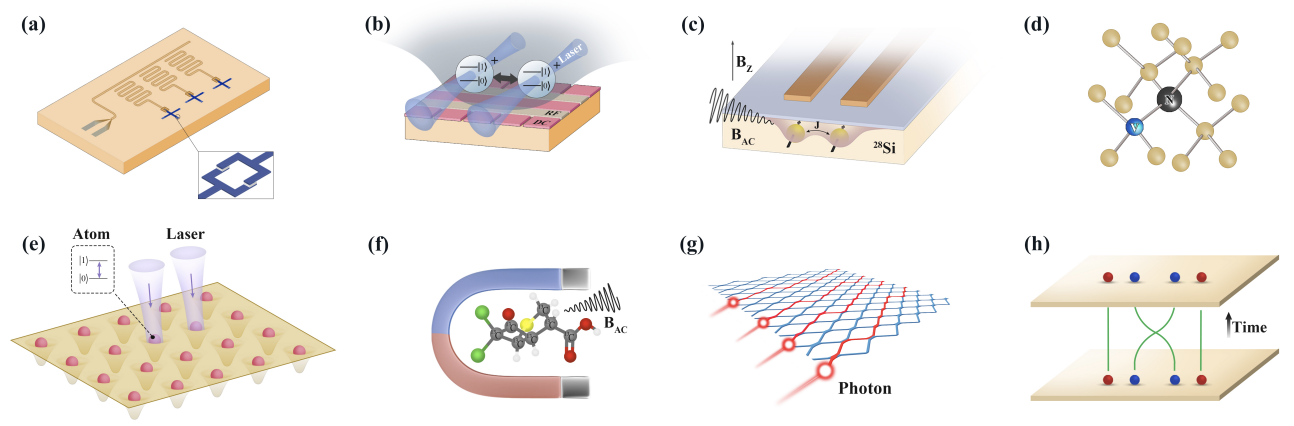
前文提到複合形式的超導量子位元,這邊簡述一些其他的量子位元。量子位元的應用上,一方面要求量子位元要容易控制,一方面也希望量子位元不容易受到雜訊干擾、延長退相干時間。然而目前這兩個需求是衝突的,容易控制意味著易受影響、反之穩定度高意味著難以控制。
因為不同量子位元的種類有不同的特性,發展在同一個整合不同的量子位元、甚至是複合量子位元,便是一個可行的方向。
Ref: arxiv: 2303.04061
(a) 超導量子處理器 (Superconducting Quantum Processor)
由約瑟夫森結與電容組成的人工原子陣列,透過微波電子學進行控制。
Qubit數量:~100
Quantum Gate保真度:
Single Qubit Gate \( F_1 > 99\% \),2 Qubit Gate \( F_2 > 99\% \)
優勢:快速操作、高度可控性與良好可擴展性
挑戰:串擾、高冷卻需求、大規模擴展挑戰
(b) 捕獲離子量子計算 (Trapped Ion Quantum Computing)
利用雷射冷卻的原子離子,透過射頻電場捕獲,並用雷射操控。
Qubit數量:20–30
Quantum Gate保真度:
Single Qubit Gate \( F_1 > 99.9\% \),2 Qubit Gate \( F_2 > 99\% \)
優勢:超長相干時間、高精確度、可重新配置連結
挑戰:技術上難以進行大規模整合
(c) 半導體自旋量子計算 (Semiconductor Spin-Based Quantum Computing)
利用半導體量子點中的電子或空穴自旋作為Qubit。
Qubit數量:6
Quantum Gate保真度:
Single Qubit Gate \( F_1 \approx 99.99\% \),2 Qubit Gate \( F_2 \approx 99.5\% \)
優勢:技術成熟、相干時間長、小占用空間
挑戰:需納米級製造精度
(d) NV 中心量子計算 (NV Center Quantum Computing)
在鑽石中的點缺陷,利用電子與核自旋的長相干時間進行運算。
Qubit數量:10
Quantum Gate保真度:
Single Qubit Gate \( F_1 \approx 99.995\% \),2 Qubit Gate \( F_2 \approx 99.2\% \)
優勢:可在室溫操作、高靈敏度、適用於量子網路
挑戰:難以大規模擴展
(e) 中性原子陣列量子計算 (Neutral Atom Array Quantum Computing)
利用光鑷捕獲中性原子,透過 Rydberg 作用控制原子相互作用。
Qubit數量:
數位處理器:24
類比模擬器:289
優勢:同時支持數位運算與類比模擬,具良好擴展性
挑戰:2 Qubit Gate保真度需提升
(f) 核磁共振 (NMR) 量子計算
使用分子中的核自旋進行運算。
Qubit數量:12
Quantum Gate保真度:
Single Qubit Gate \( F_1 \approx 99.98\% \),2 Qubit Gate \( F_2 \approx 99.3\% \)
優勢:室溫操作、長相干時間、適用於數位模擬
挑戰:難以擴展至大規模系統
(g) 光量子計算 (Photonic Quantum Computing)
透過單光子或電磁場模式的共軛變數來操控量子資訊。
Qubit數量:18(具個別控制)、255(九章 3.0)
Quantum Gate保真度:
Single Qubit Gate \( F_1 \approx 99.84\% \),2 Qubit Gate \( F_2 \approx 99.69\% \)
優勢:抗退相干能力、室溫操作、適用於分佈式計算
挑戰:光子-光子閘難以實現
(h) 拓撲量子計算 (Topological Quantum Computing)
基於non-abelian Anyon 的拓撲編碼,透過編織操作進行運算。
Qubit數量:實驗中
Quantum Gate保真度:N/A
優勢:天然拓撲保護機制、大規模糾錯潛力
挑戰:尚在發展中
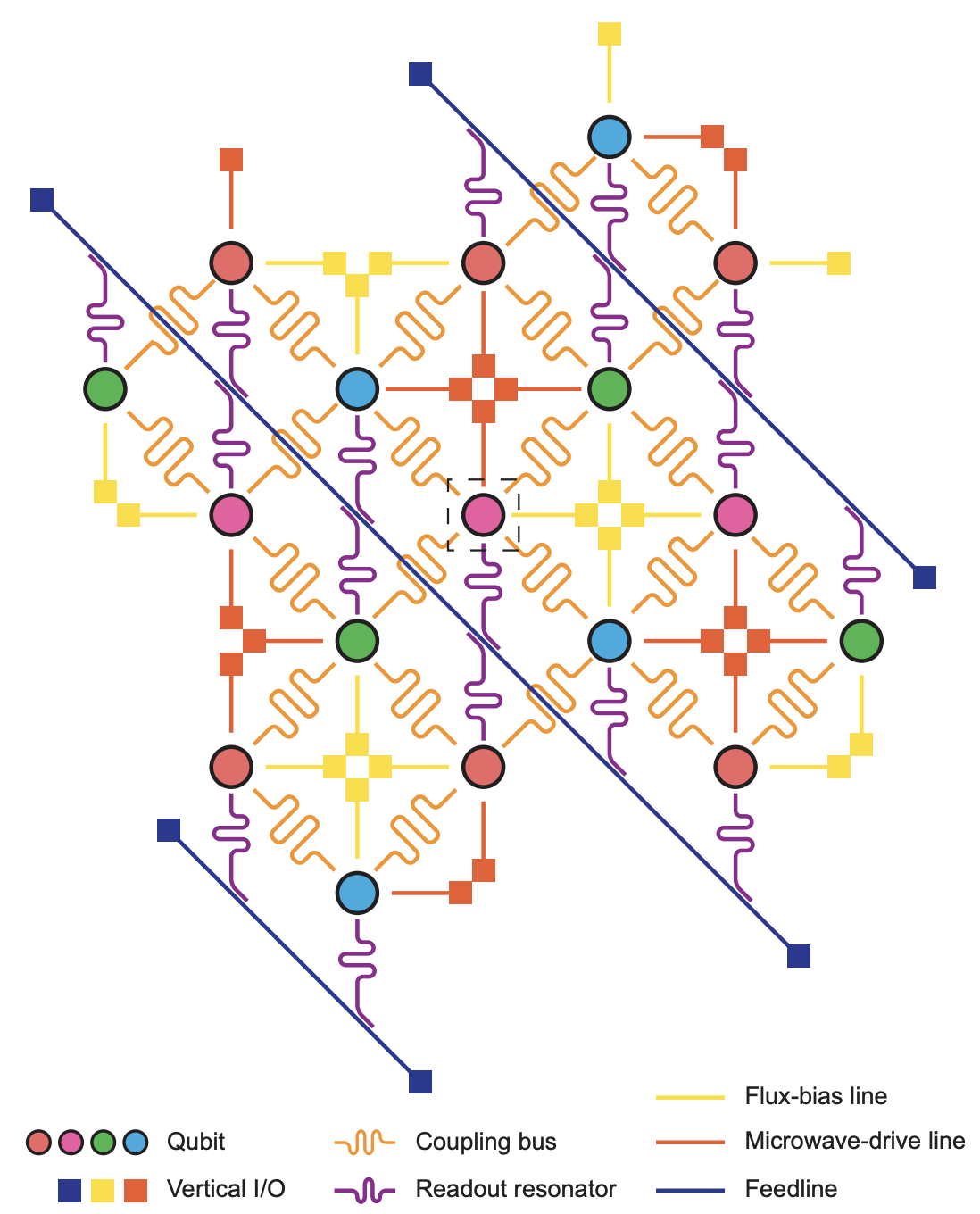
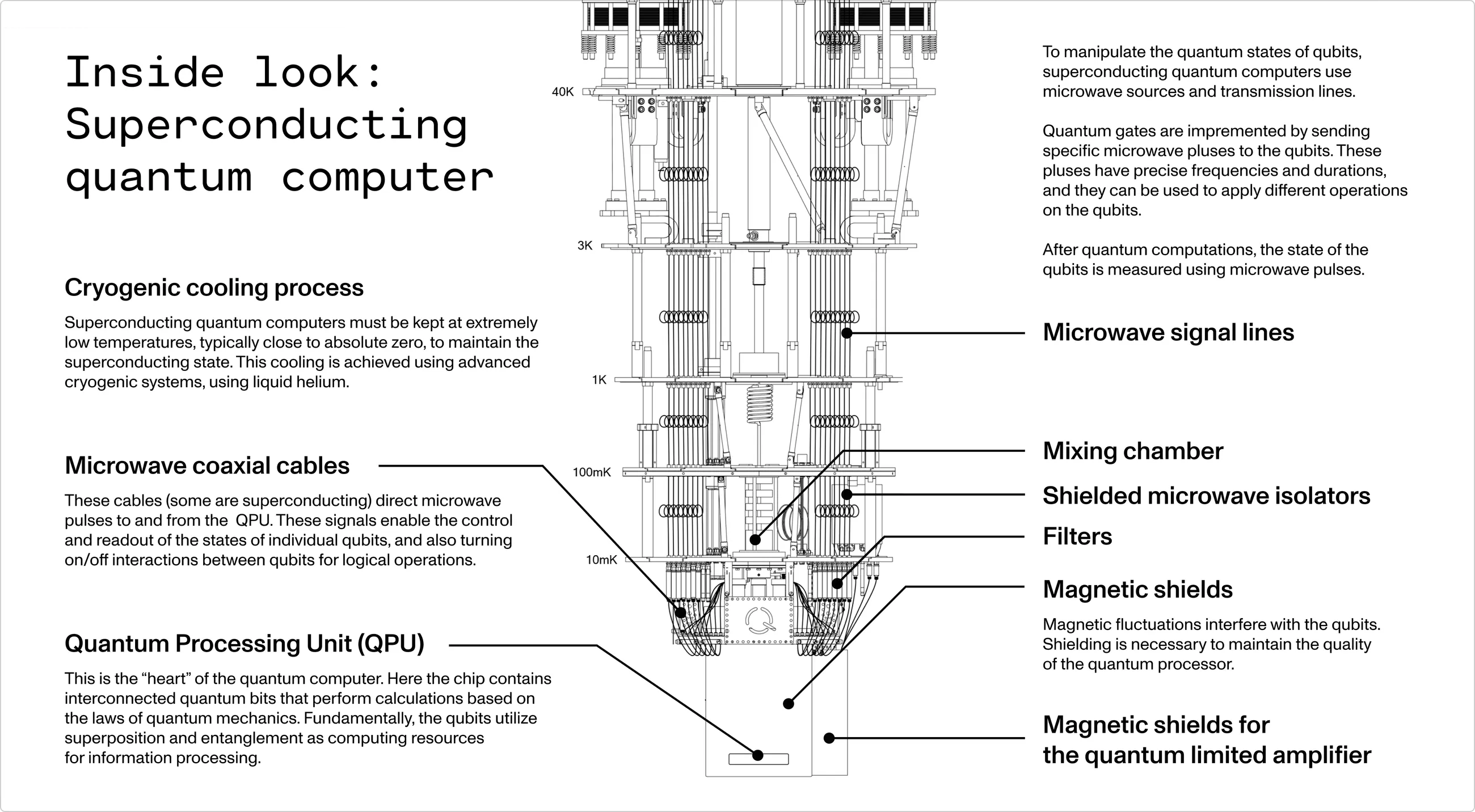
完整的超導量子電腦至少需包含:氦3極低溫真空環境、冷卻系統、大量的射頻訊號控制與讀取儀器等,故當前的超導量子電腦非常的巨大。此外,一個量子位元至少需要四條線路:
https://arxiv.org/pdf/1612.08208
▲要達到量子計算,需要同時操作許多 Qubit,同時因為糾錯的關係,也需要額外的 Qubit 來進行糾錯。上圖是一個 17 位元的實驗性量子晶片,排列方式是一種稱為 surface code(表面碼)的量子糾錯型態,原形為 Qubit,粉色及紅色是 Data Qubit,天藍色及綠色是 Check Qubit。每個 Qubit 都連接 7 條線(暱稱為 Starmon),其中 4 條為 Qubit 間耦合、1 條 Flux line、1 條 Drive line、1 條 Readout resonator。Readout resonator 分別併入到三條 feedline。雖然當前的技術可以將多個Qubit的Readout line整合在一起,透過頻率隔離的技術共用同一條Readout line(所謂Feedline),但我們還需要考慮控制量子位元間交互作用的Resonator,一個100位元的量子電腦原型就需要400條線路從外部送入,故目前常見的超導量子電腦可以看見大量的線路。
arxiv: 2408.12433
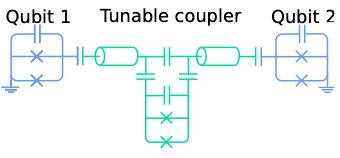
量子位元間交互作用的Resonator/Coupler可以是可調控的,可進一步調控不同Qubit之間的耦合強度,但亦會增加控制電路的複雜度。
Ref: IBM
Ref: Google
Ref: IQCC and Quantum Machines
▲IQM公司繪製出量子電腦低溫腔內的細節設計圖。
Ref:
IQM
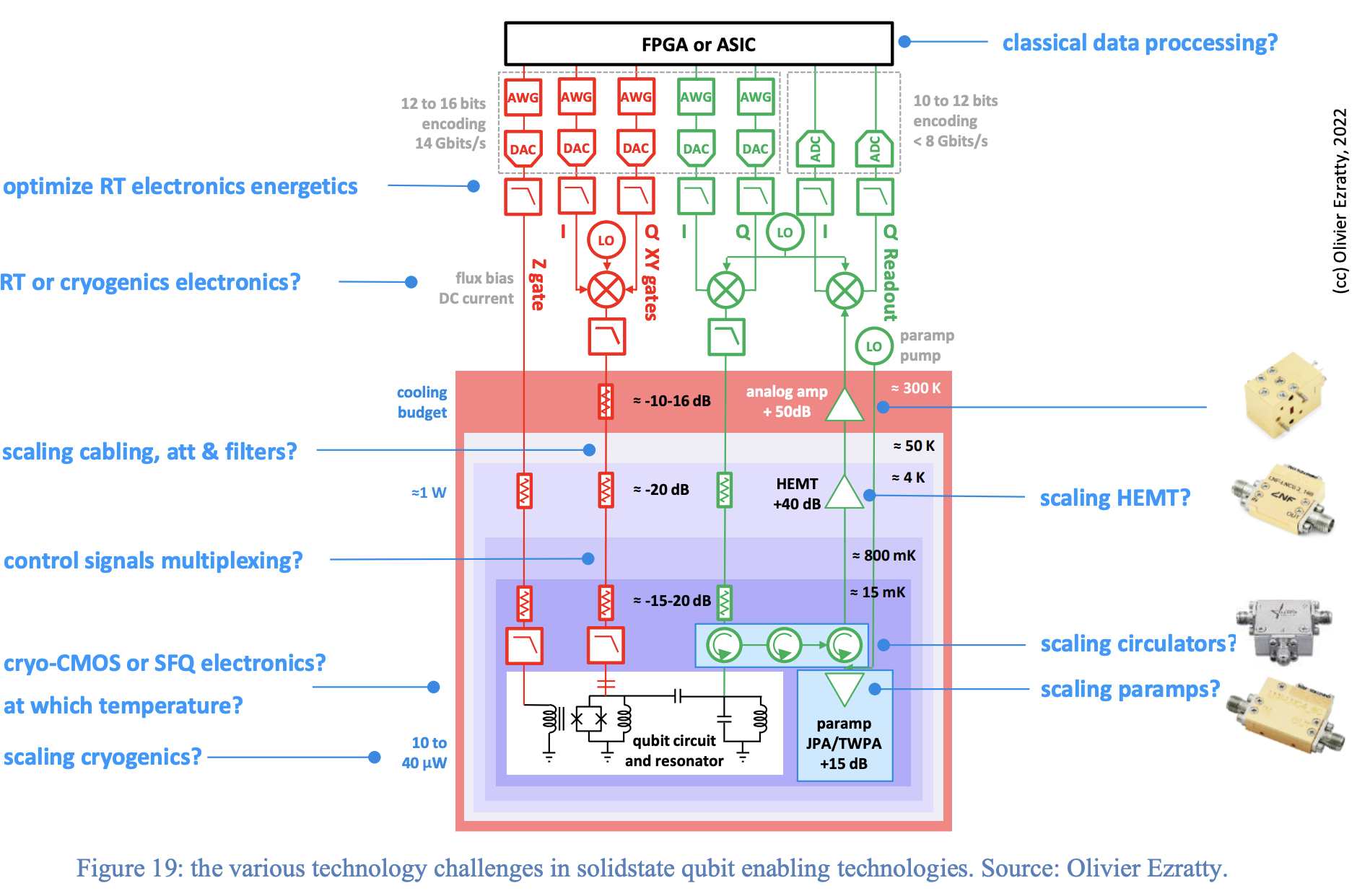
前文介紹量子電腦複雜的硬體設計,本節稍微介紹一下超導電腦控式訊號的線路設計。控制訊號由任意波形產生器(AWG)生成數位訊號,透過數位-類比轉換器(DAC)轉換成類比訊號,通過層層的濾波器送入到量子位元電路中,然後回饋出來的訊號再通過類比-數位轉換器(ADC)換成數位訊號由儀器量測。
Ref: arxiv: 2303.15547
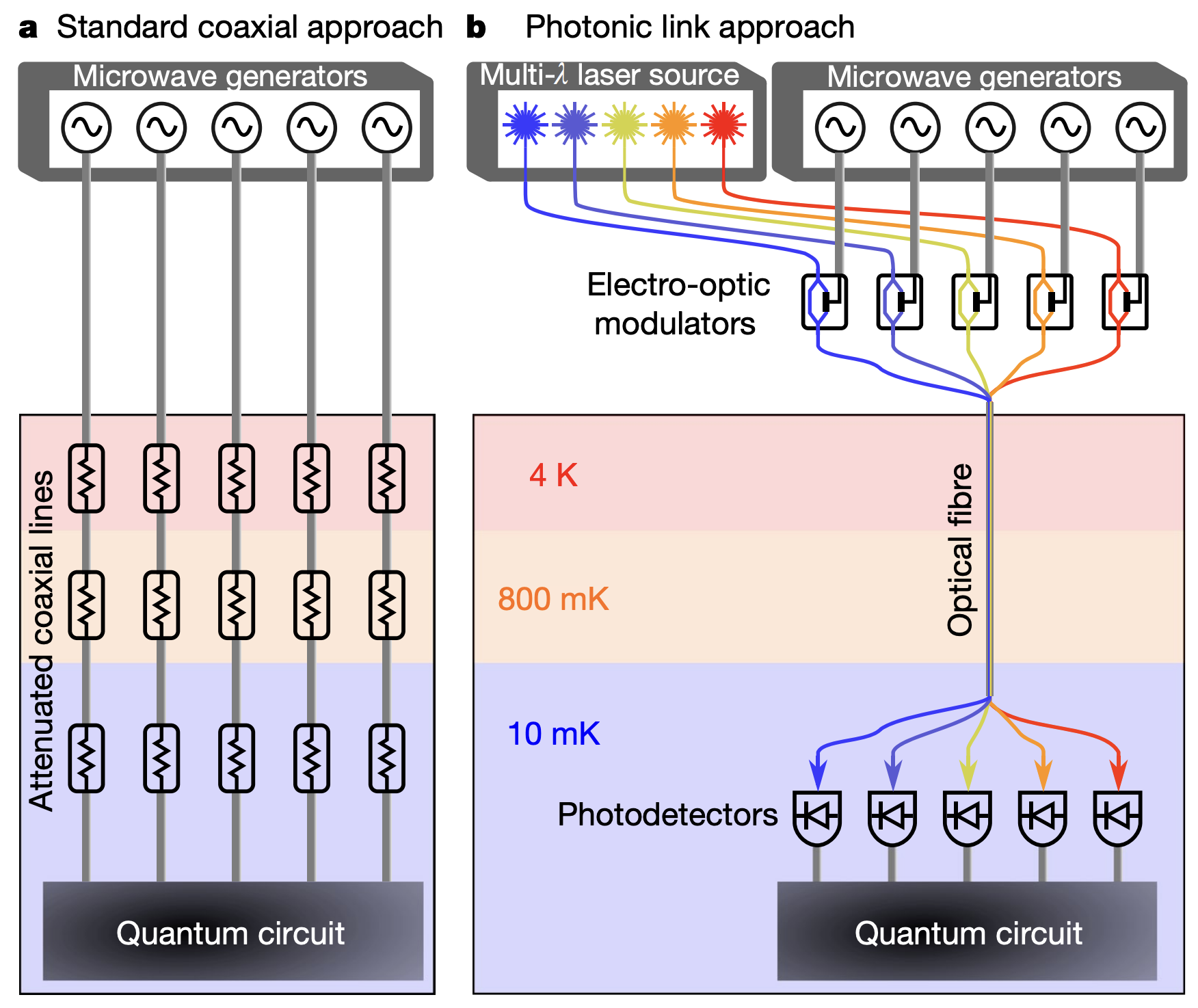
前文圖片中可以見到大量的線路層層穿越低溫腔進入到量子位元中,如此複雜的線路需要精密的設計、降噪、隔熱,容易增加成本和出錯率,造成大型化(scalable)的困難度。以下講解兩種可能的方案,試圖減少穿越的線路。
▲光纖方案,(a)是傳統控制線路,(b)採用不同波長的載波混波技術,將控制訊號透過光電轉換器放到對應的載波上,通過光纖束進入到腔體中,再轉換回控制Qubit的控制訊號。
Ref: DOI: 10.1038/s41586-021-03268-x
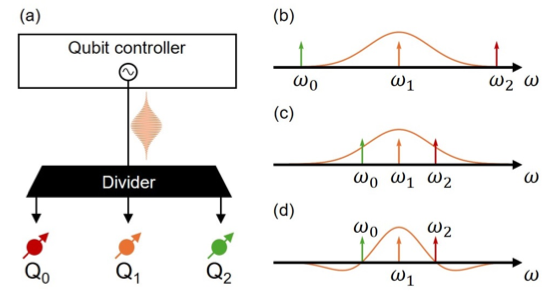
▲透過Qubit頻率隔離,並且利用設計過的控制頻譜訊號,使得Qubit之間的控制可以隔離開來,便可通過單一控制線路控制多個Qubit。
arXiv:2501.10710v1
在這邊簡單提一下量子處理器QPU設計。當前量子電路是二維電路,Qubit間的交互作用在電路上常只能與鄰近的Qubit連接。再搭配目前常見的糾錯設計(QEC)是表面碼(Surface code)採用四邊形的設計,所以當前的QPU,每個Qubit僅需四個coupler與鄰近Qubit耦合。製造商IQM亦提供新的QPU設計,試圖加入Computational Resonator,構造出更進階的量子計算方式,未來有機會可以撰文解說。
Ref:
IQM
Ref: Arxiv: 2408.12433
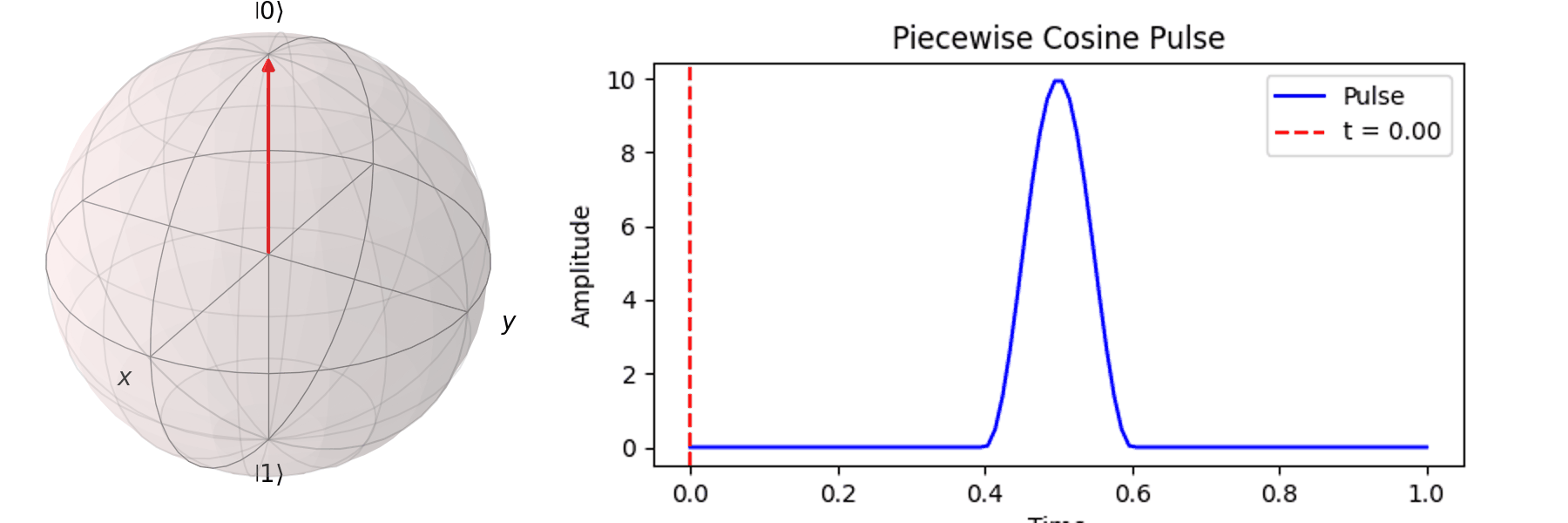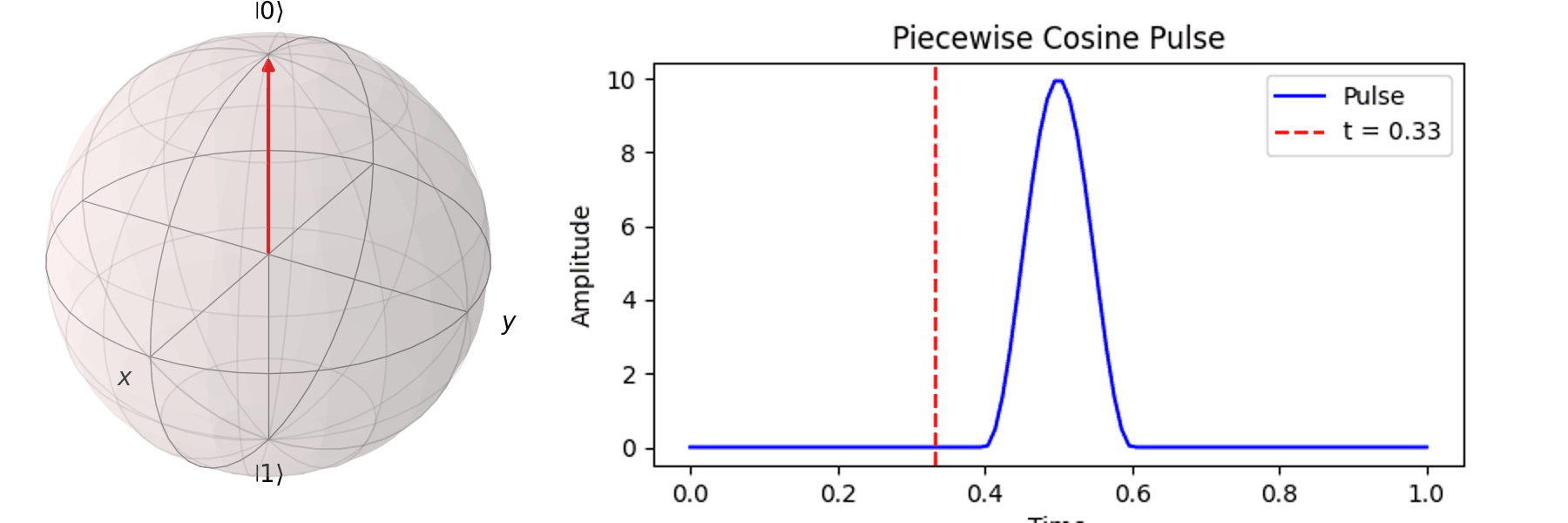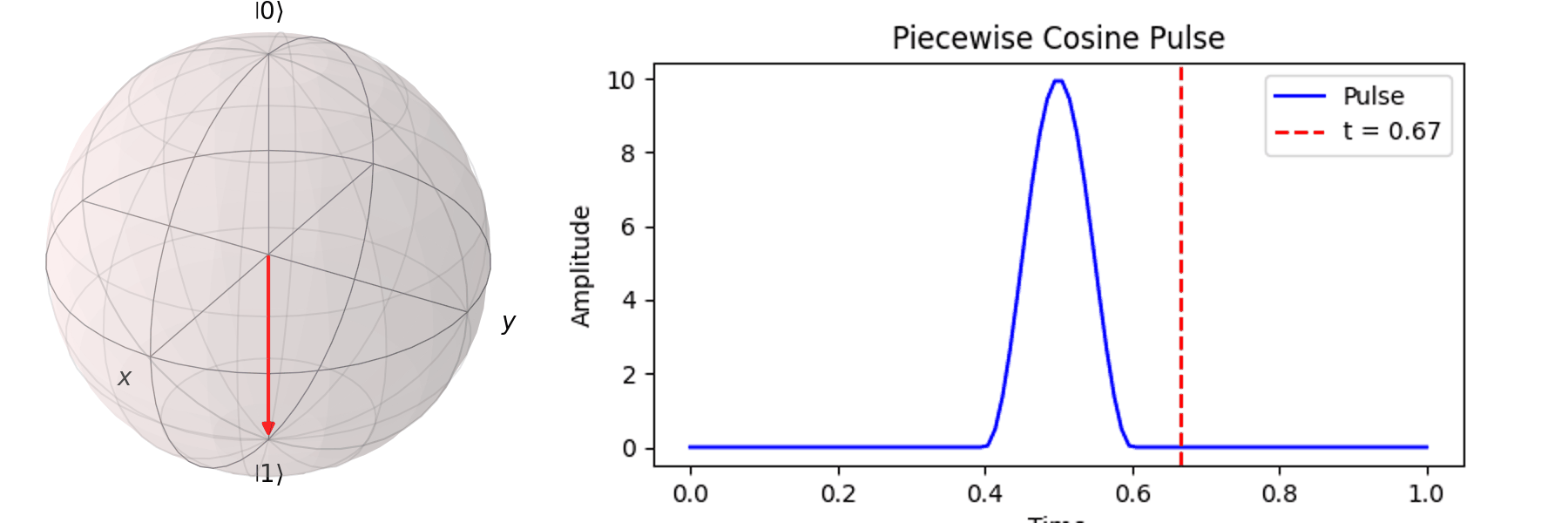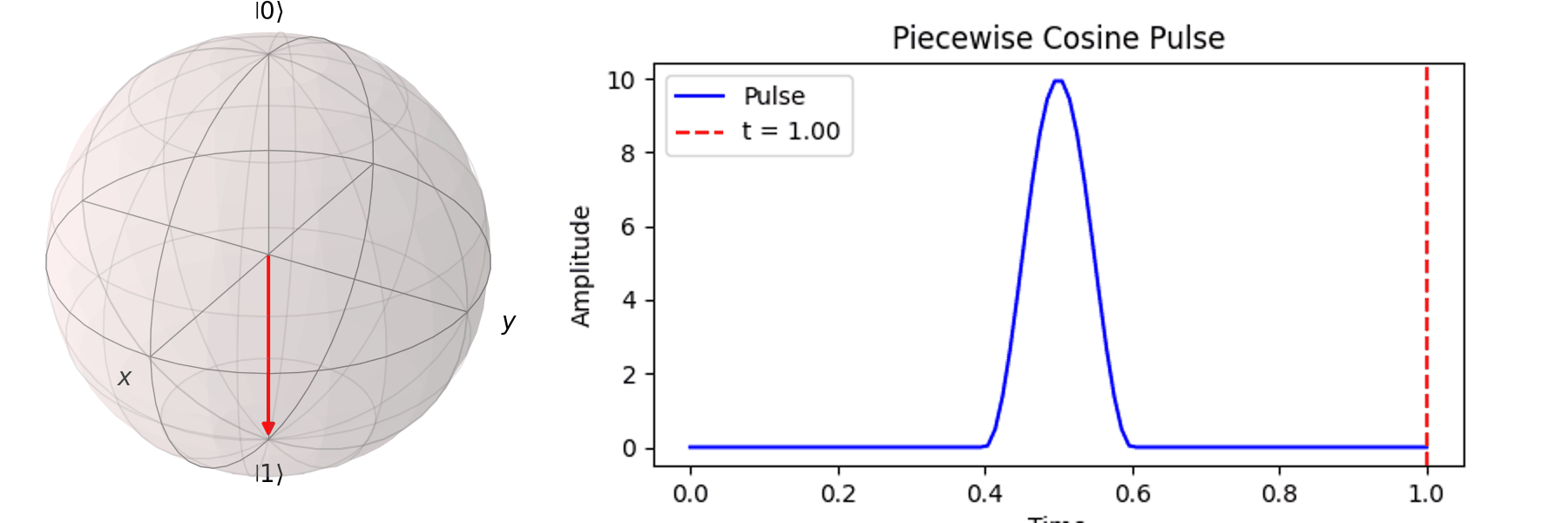
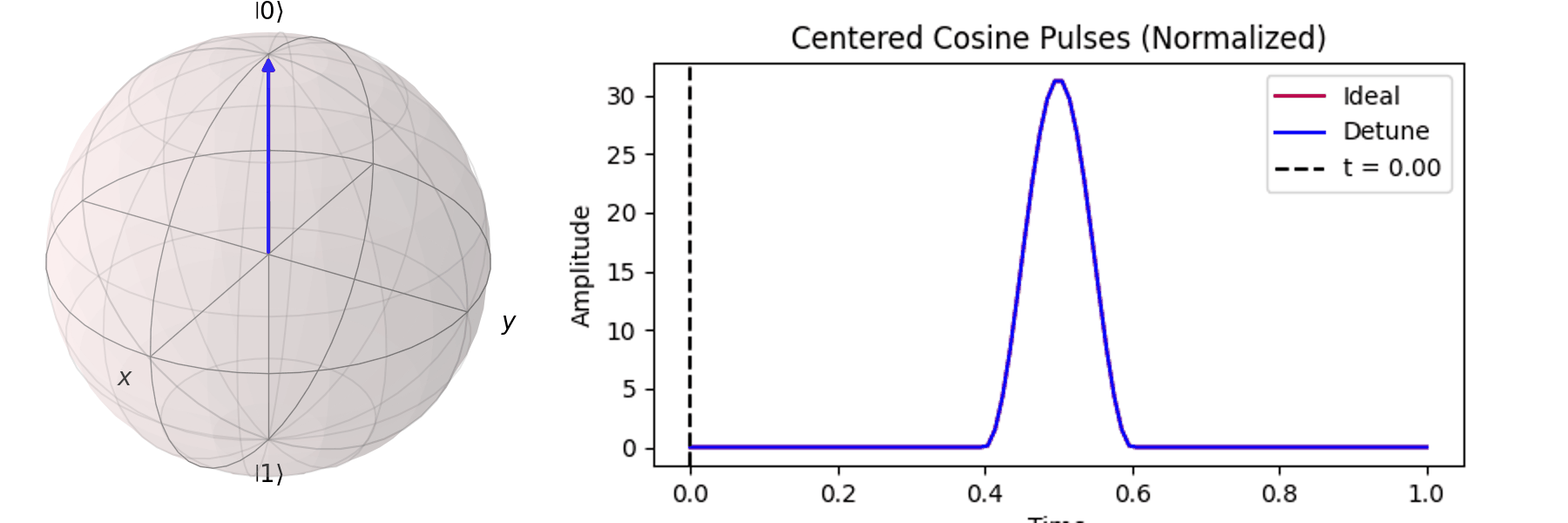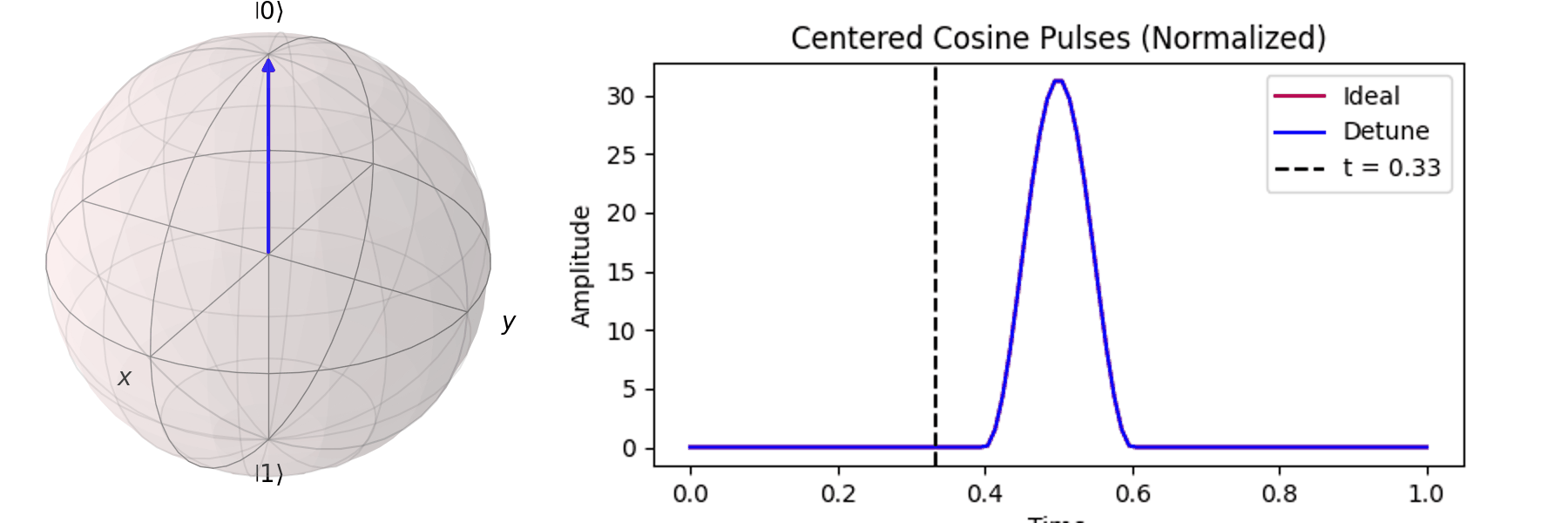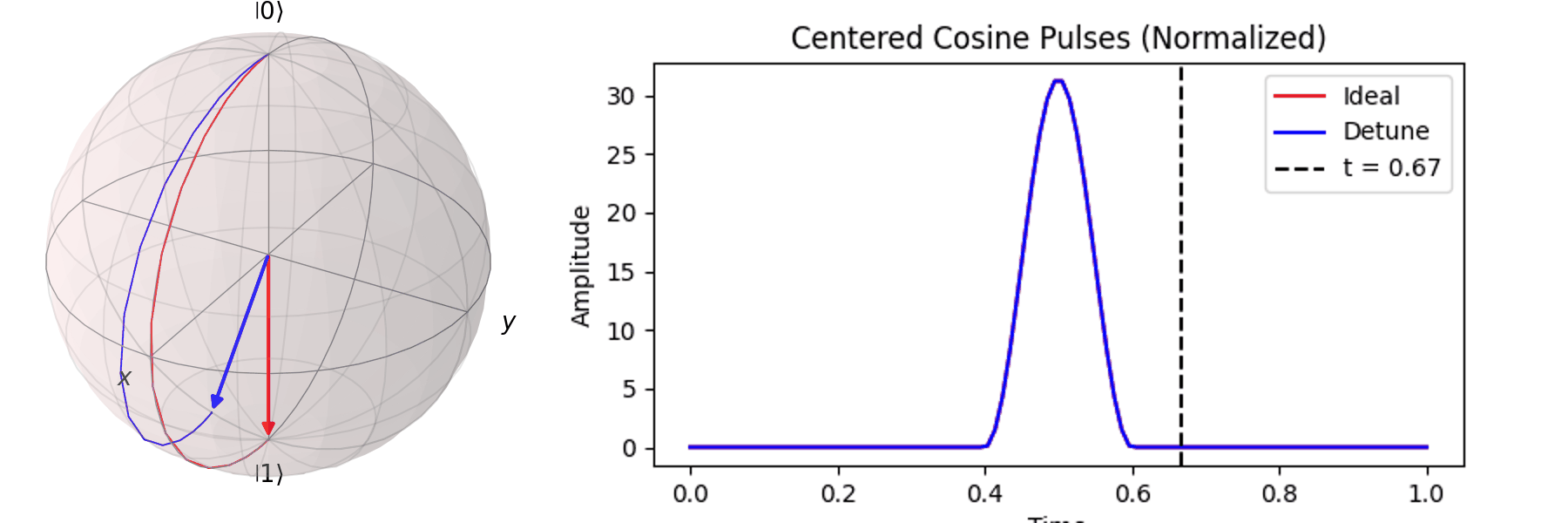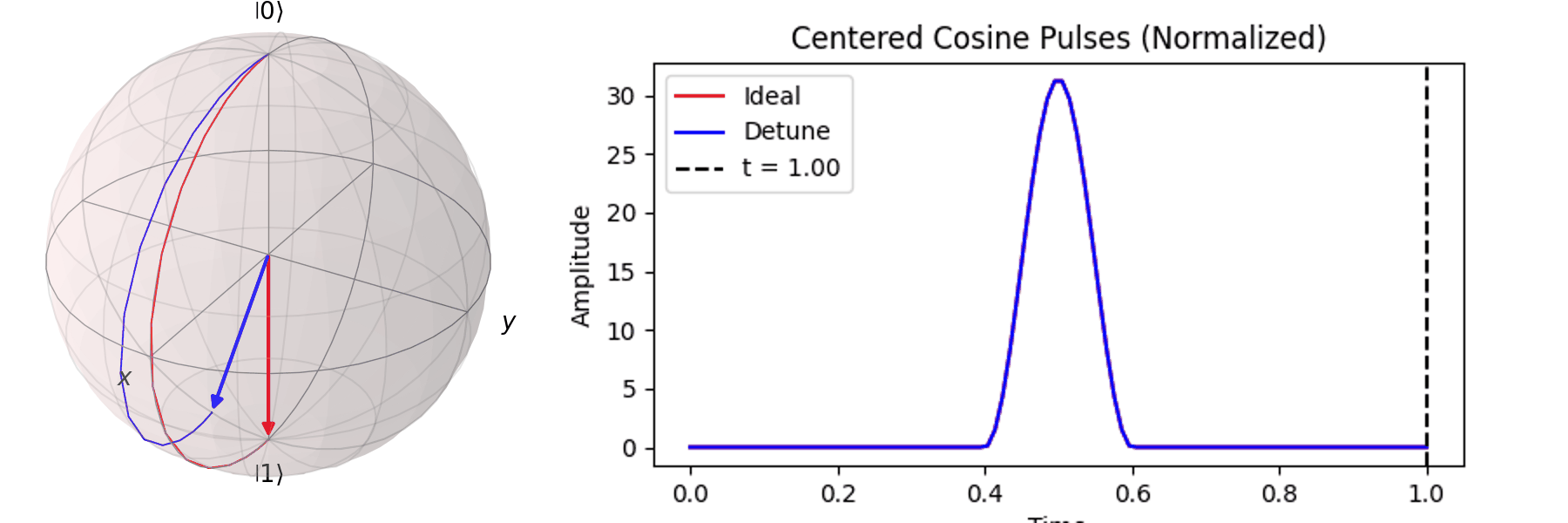
最常見的作法為拉比震盪(Rabi Oscillation),透過施加特定頻率的電場震盪脈衝(Pulse) \( P(t) \)。先來看 Qubit 受到 \( \pi \) -pulse從 \( |\ 0\rangle \rightarrow |\ 1\rangle \),利用 Bloch 球進行可視化:
控制 Qubit 的主要參數
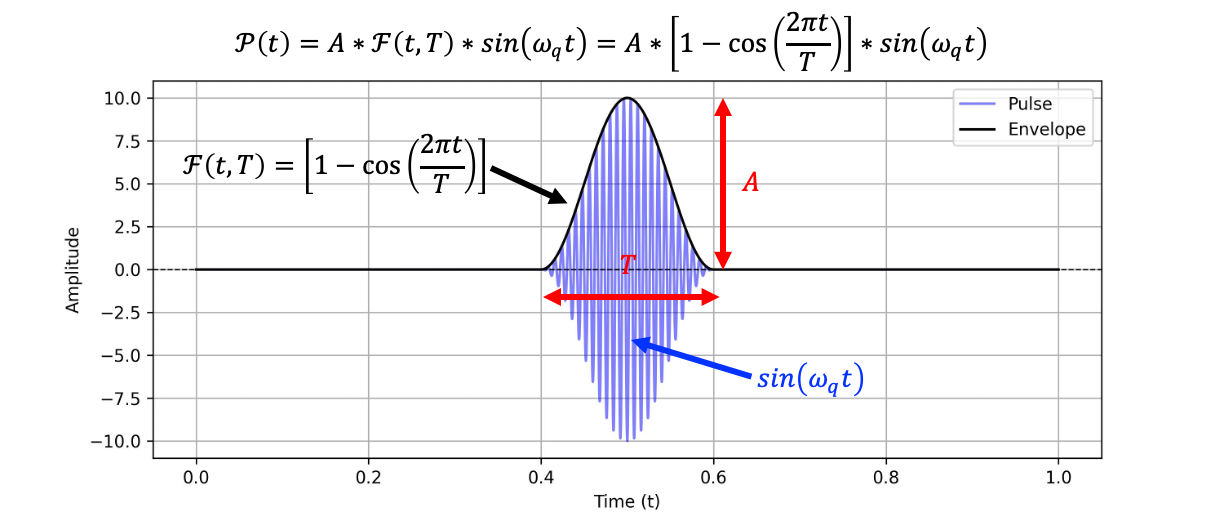
一般來說因為Qubit相干時間很短,會希望盡可能短的時間操作完Qubit的運算,以超導量子位元而言,相干時間能維持達微秒(μs)當前的技術而言已經很久了,故超導量子位元脈衝多半固定在奈秒等級(\(ns\))。故操作Qubit的狀態一般採用調控脈衝的振幅的大小來決定轉角。
(以10.1103/PRXQuantum.5.030353為例,實驗中驅動大約\(10ns\)左右)
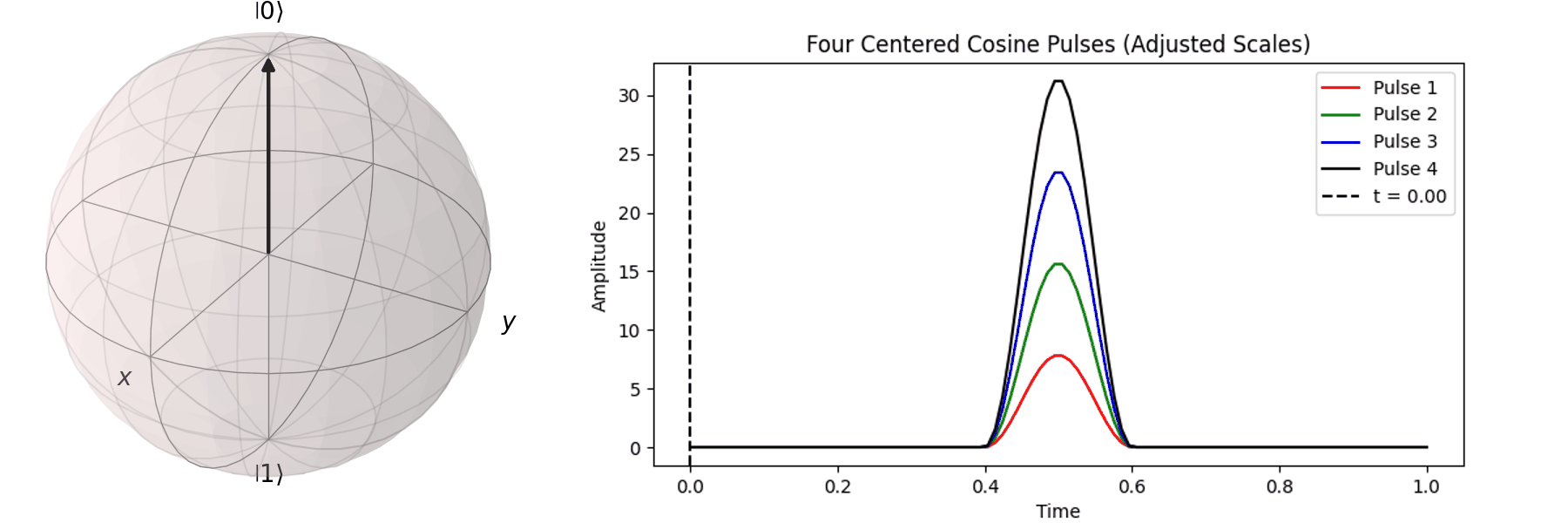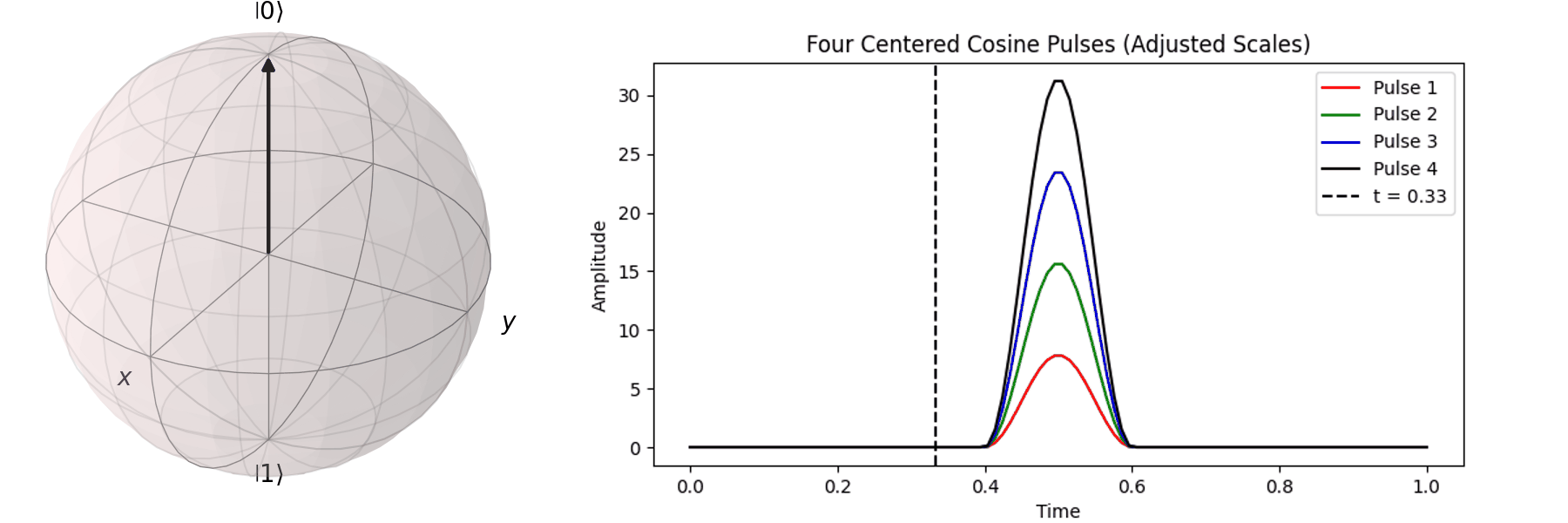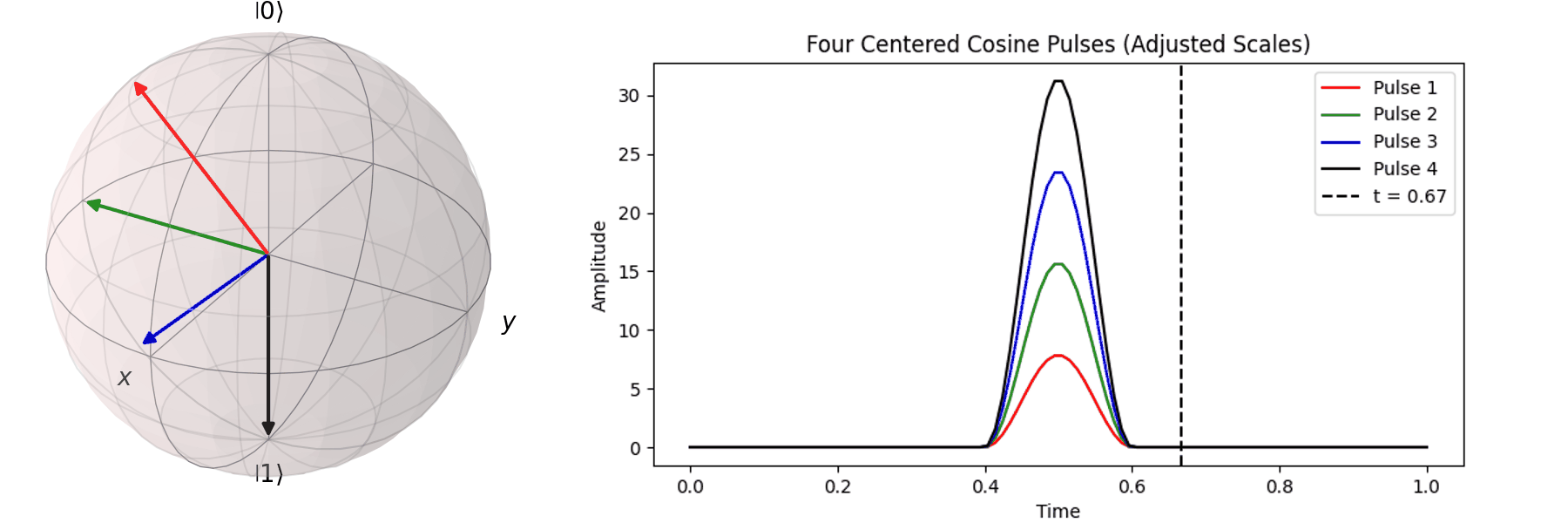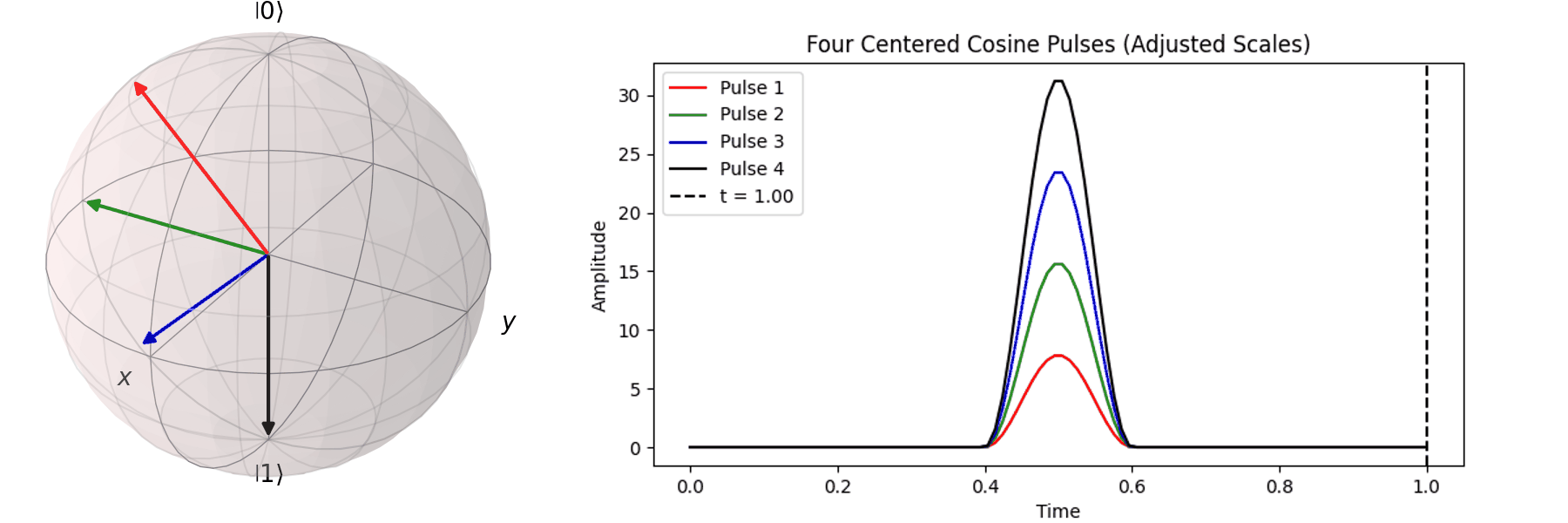
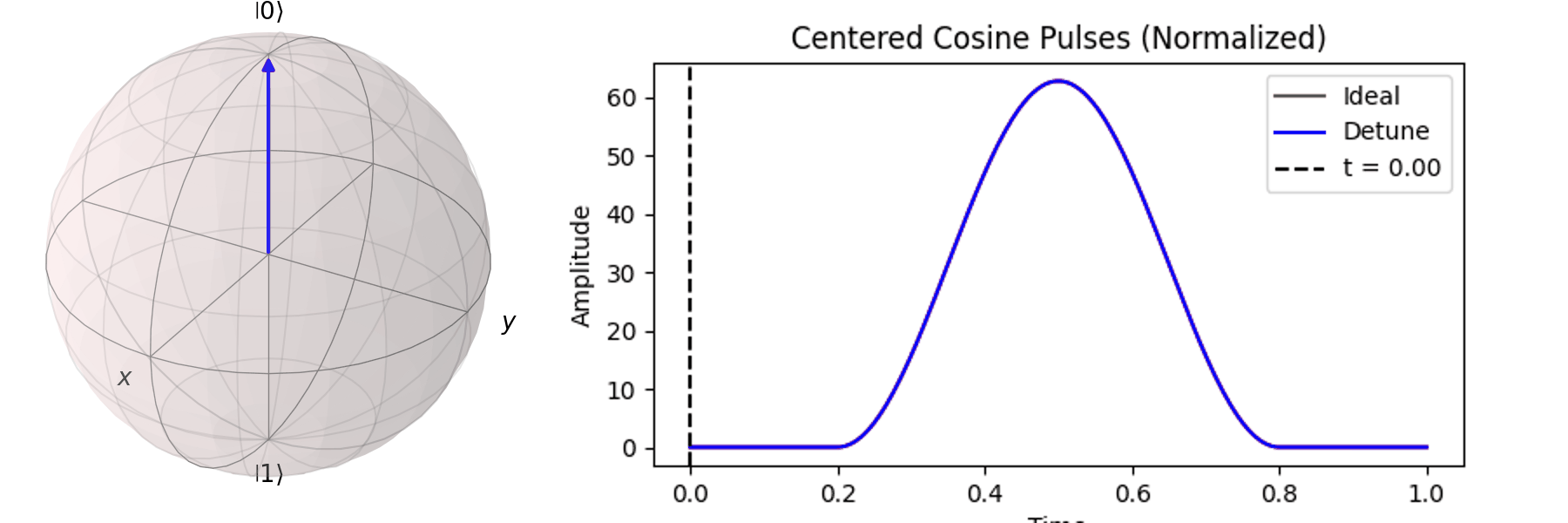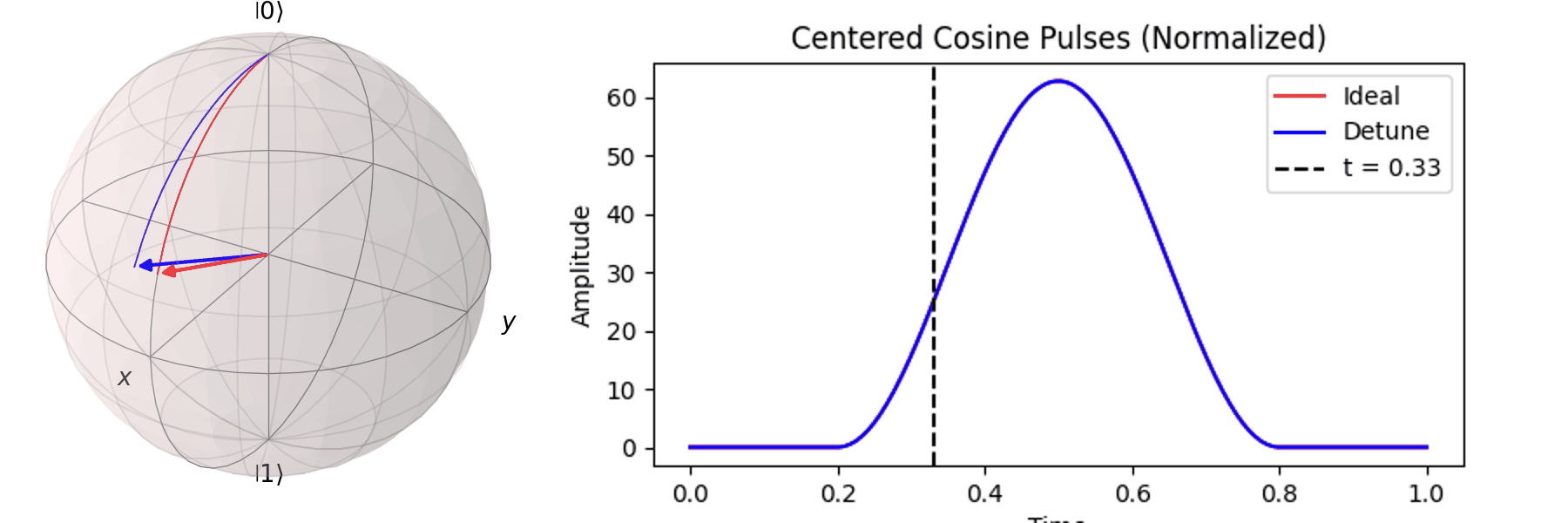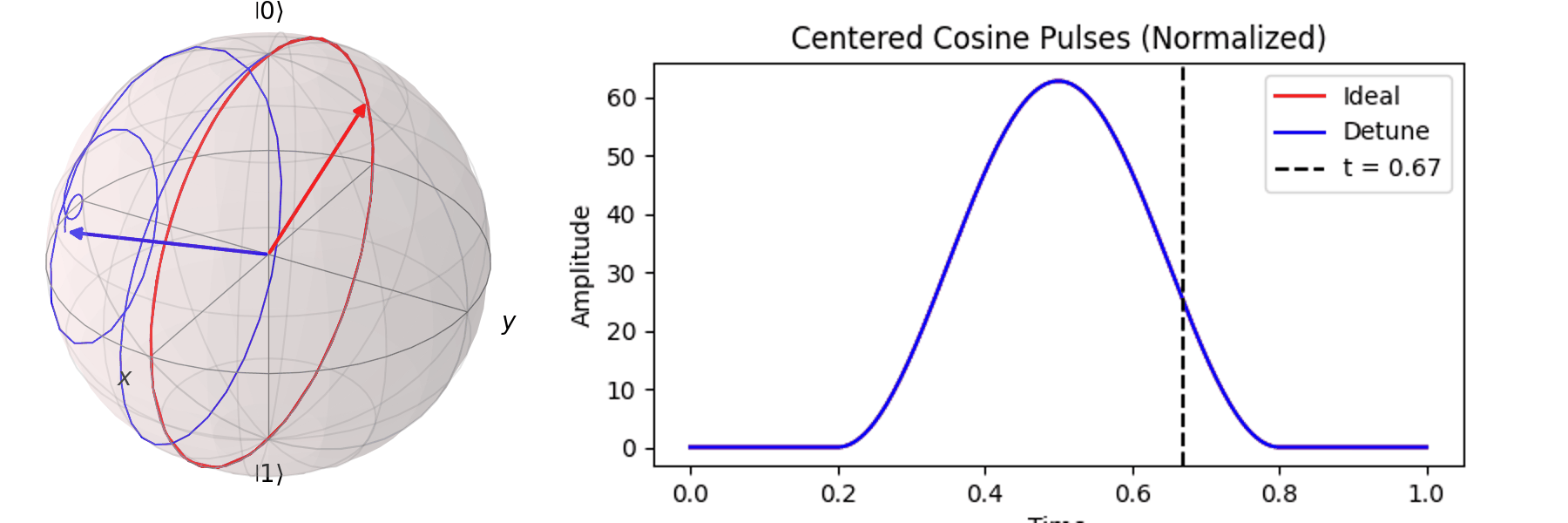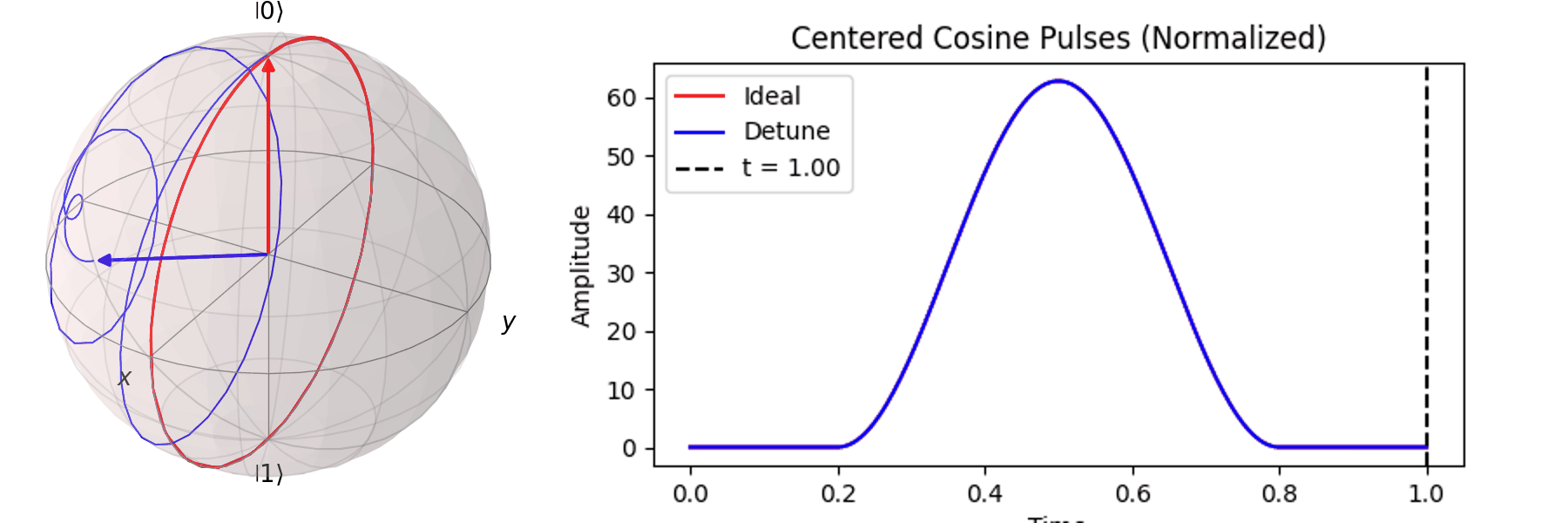
可以藉由 Bloch 球進行可視化,在這邊畫出對\( X \) 軸轉 \(0.25\pi \)、\( 0.5\pi \)、\(0.75\pi\)和\(\pi\)-pulse。可以發現說利用振幅的大小可以決定轉動的角度。
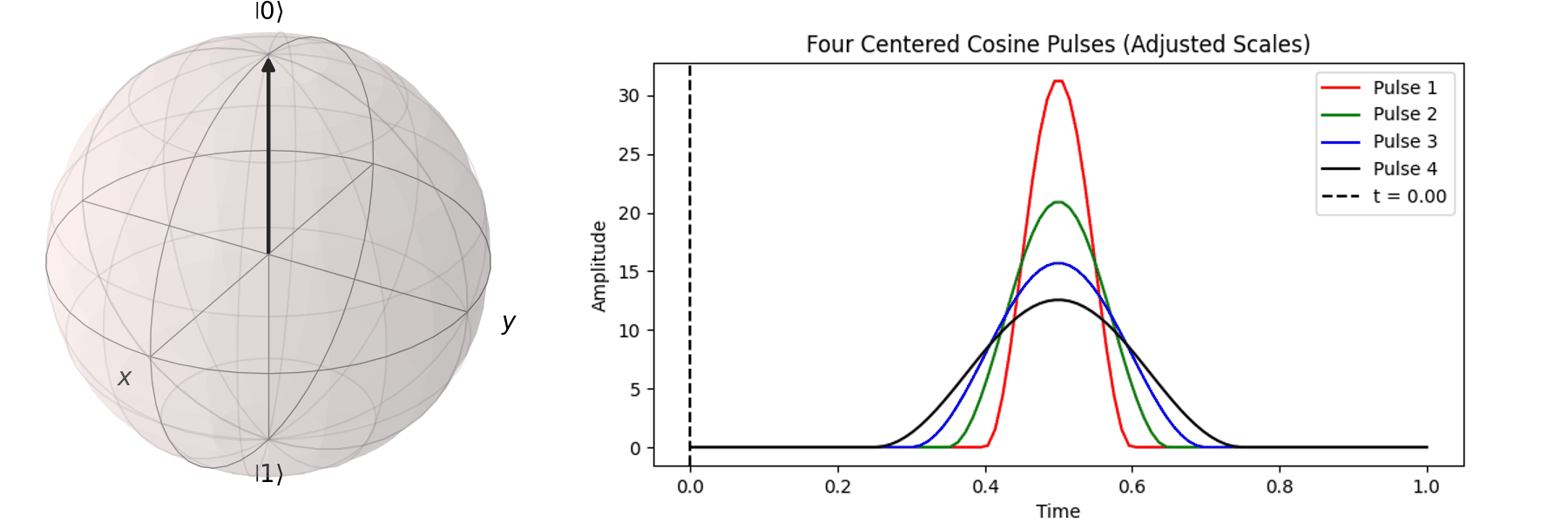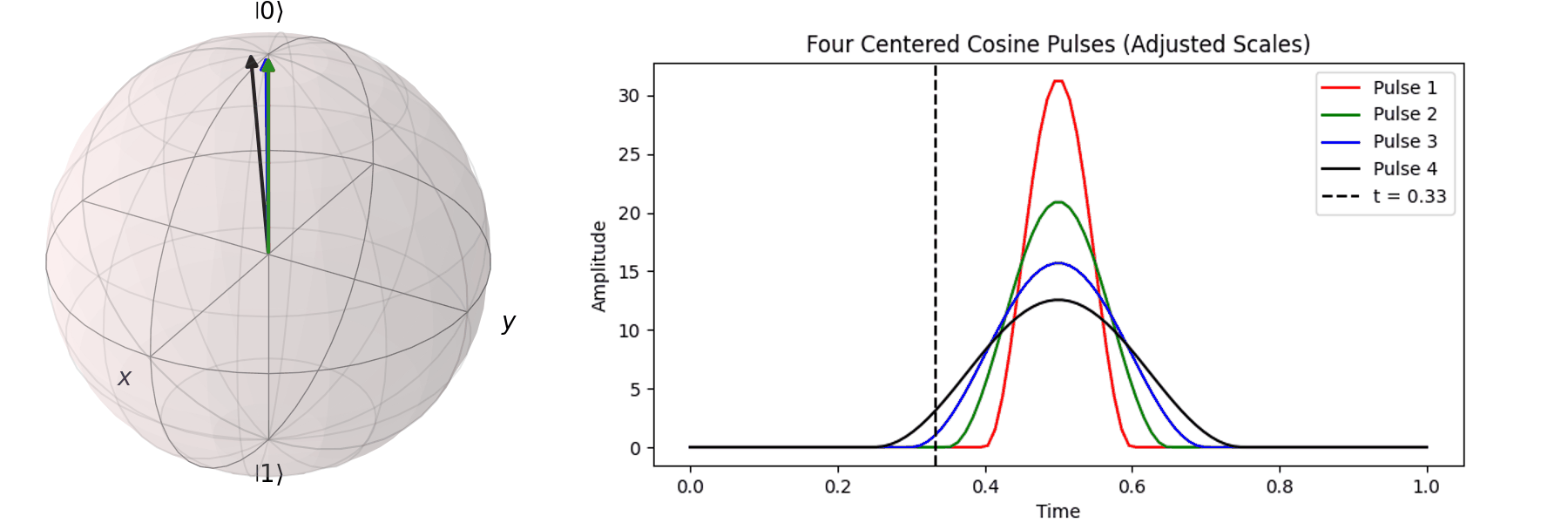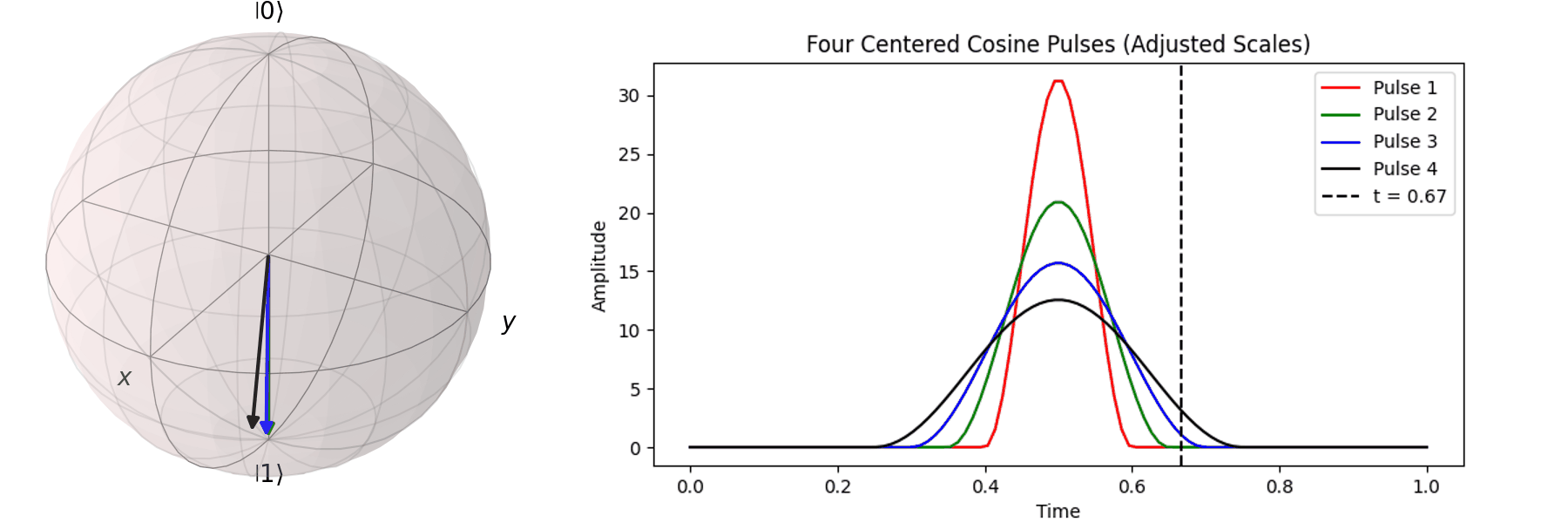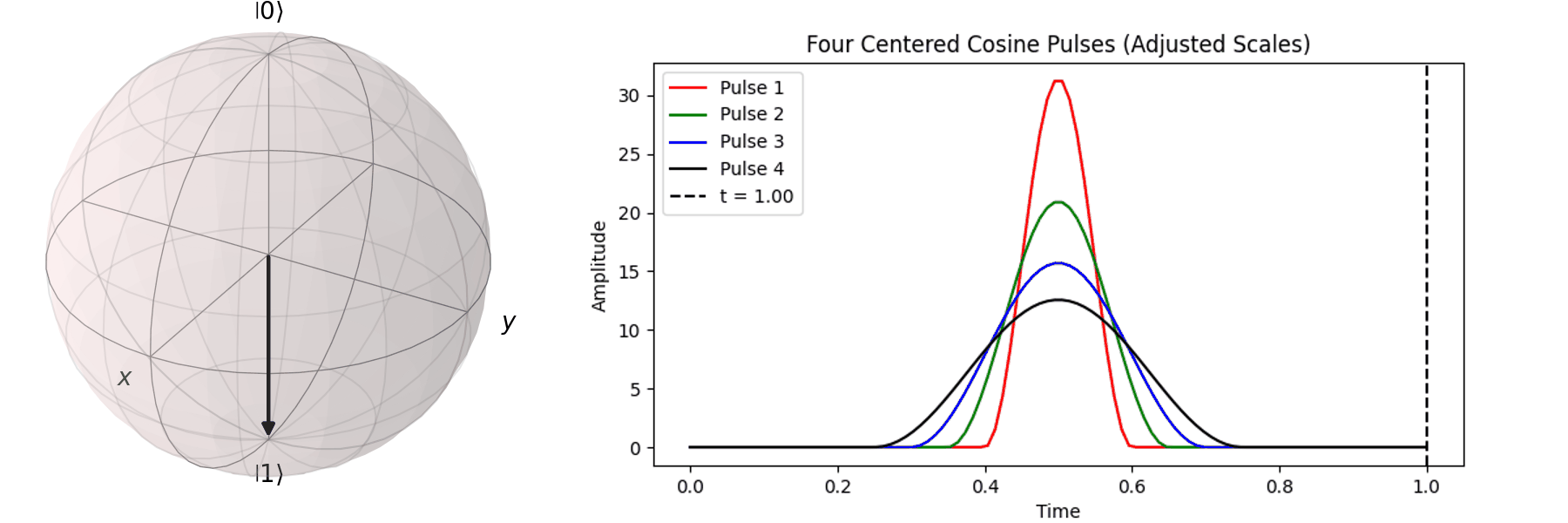
同樣的,也可以討論利用不同脈衝的時長\(T\)來達到相同的 \( \pi \) -pulse從 \( |\ 0\rangle \rightarrow |\ 1\rangle \)
當然,讀者也許會想說,既然超導Qubit相干時間很短,那脈衝的時長\(T\)越短越好。下一節我們就會提到,越尖的脈衝會引入更多不相關的震動頻率,導致Qubit的操作出現誤差。實務上,如何決定脈衝的時長\(T\)與脈衝的震幅\(A\),一直是Qubit日常校正的一環。良好的校正會得到優質的量子計算效果,反之,光是誤差就可以導致計算不如古典電腦來的準確。
Pulse shape:10.1103/PRXQuantum.5.030353
10.1103/PhysRevLett.116.020501
後記
Index
Contact:
![]()