超導量子位元

Author:Peir-Ru Wang
\(\to\)English Version
Update
(O04)2025.02.07：新增-計算科學與二階系統（TLS）
(O03)2025.01.18：新增-雙LC電路耦合
(O02)2025.01.12：新增-驅動 LC 電路
(O01)2024.12.29：主題建立

量子計算硬體基礎

量子計算在特定問題上蘊含遠超古典電腦的運算潛力，其硬體卻也面臨控制困難、操作時間過短的問題。量子計算的硬體以量子位元作為的核心元件，還需搭配操控量子位元狀態的驅動元件、量子位元狀態的讀取元件。此外，因為量子位元容易受到外界干擾的特性，量子位元的校正/微調元件、量子糾錯元件等。簡而言之可以包含以下：

• 量子位元
• 驅動
• 讀取
• 校正
• 糾錯

事實上，在現今的記憶體中，其實也包含以上不同的硬體分工，只是在量子計算裡面，以上不同元件需要整體考慮。更具體一點的講法，因為不同元件會互相交互作用，當我們利用量子物理學，寫下其整個量子電路的 Hamiltonian（或薛丁格方程式），其交互作用像會去"修正"量子位元本身的特性，一方面我們利用"修正"的特性來操作和讀取量子位元的資訊，然而另一方面卻也導致量子位元受到影響，偏離理想狀態、導致錯誤產生。

本文專注在超導量子電路，量子電路中包含的元件分類如下（兩種切入點）：

以功能性為觀點	1. 量子位元（資料儲存） 2. 驅動：耦合電路或 LC 共振器（作運算） 3. 讀取（readout）：LC 共振器與饋線 4. 校正：Flux line（改變量子位元頻率） 5. 糾錯：量子位元（糾錯用）
以元件種類為觀點	1. LC 電路    a. LC 共振器（線性 LC 電路）：用作讀取量子位元狀態（readout resonator），有時也可以作為量子位元間耦合（間接耦合）    b. 量子位元（非線性 LC 電路）：部分作為資料儲存、部分作為糾錯用位元 2. 饋線（feedline）：外部訊號送入與讀出 3. 耦合元件：    a. 操作、改變量子位元狀態    b. 量子位元之間的直接耦合    c. 將外部訊號與各元件交換訊號 4. Flux line：調整改變量子位元頻率，讓量子位元在指定頻率運作



arxiv.org/pdf/2106.11352
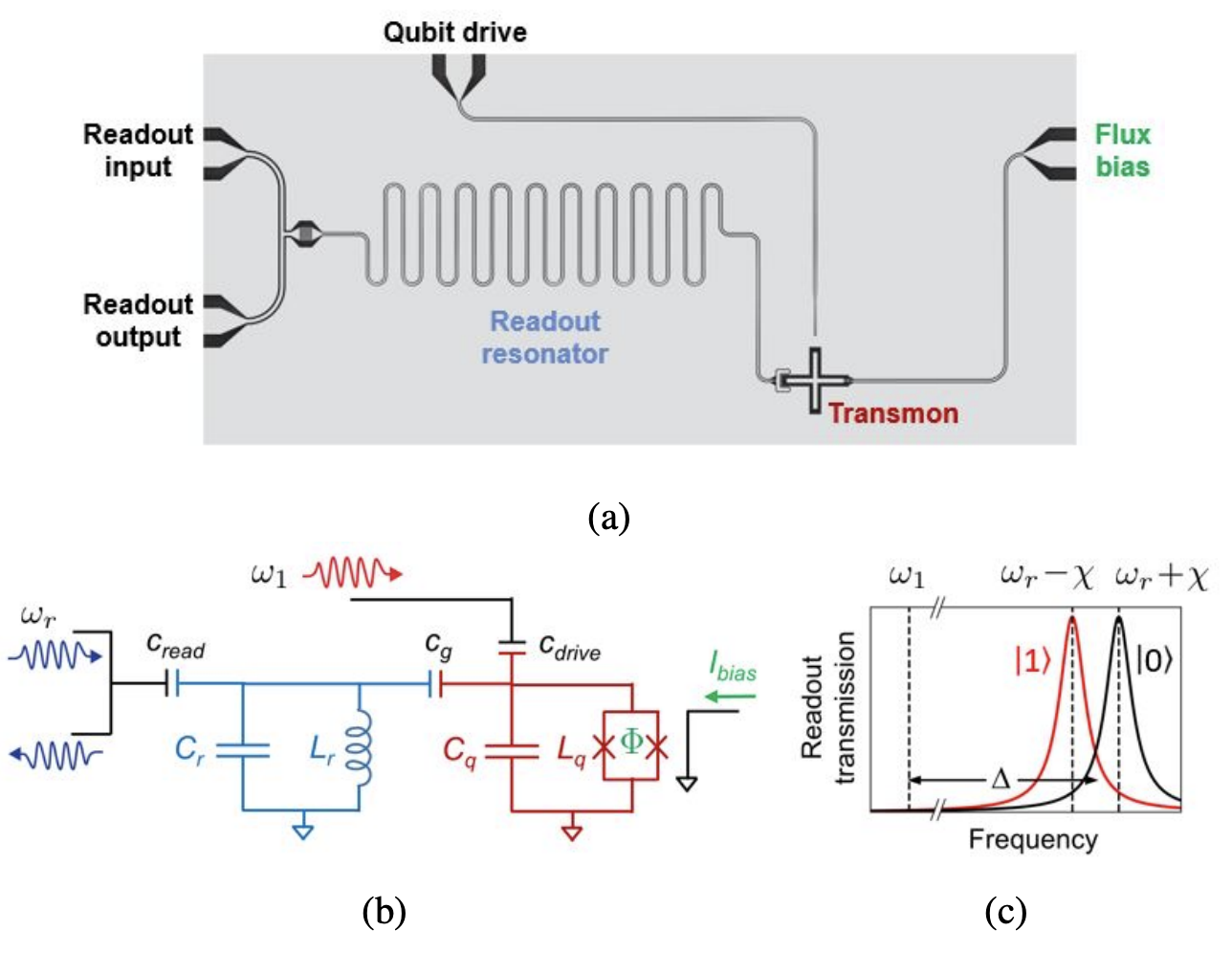
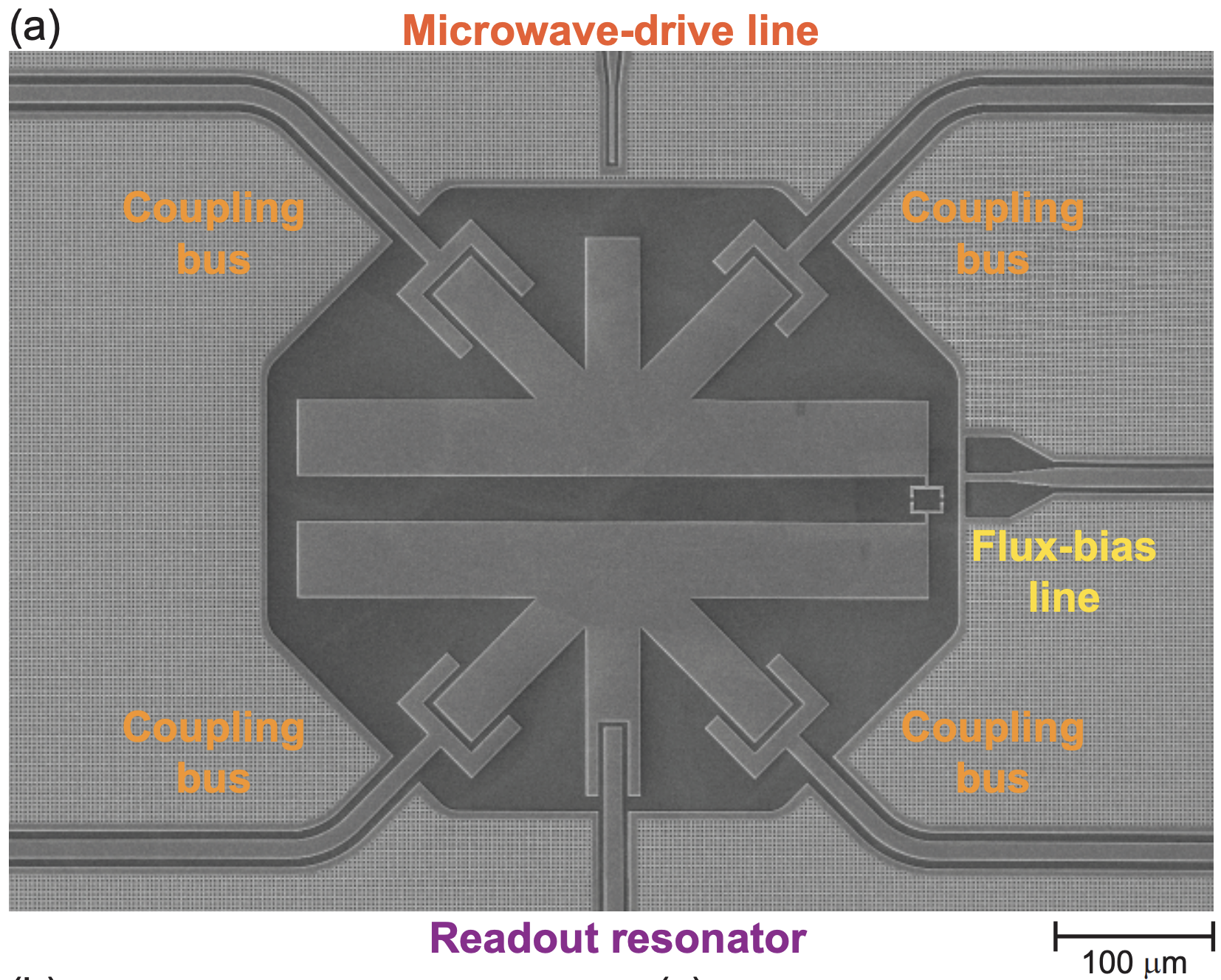
首先可以先欣賞一下單量子位元的 layout。（a）顯微鏡底下的電路圖，（b）對應的電路圖，此圖中有一個 Qubit（紅色 Transmon）、一個 readout resonator（天藍色），兩條 feedline 個別驅動（Drive）量子位元與 readout resonator。各元件間利用電容作耦合。另外有一條 Flux line 連到 Qubit 旁，會產生磁場來改變 Transmon 的操作頻率。（c）readout resonator 因為與量子位元耦合，會受到量子位元在 \(|0\rangle\) 或 \(|1\rangle\) 狀態的差異產生頻譜的位移，利用 readout resonator 頻譜的位移的特性來得知量子位元的狀態。



doi.org/10.1038/nature08121
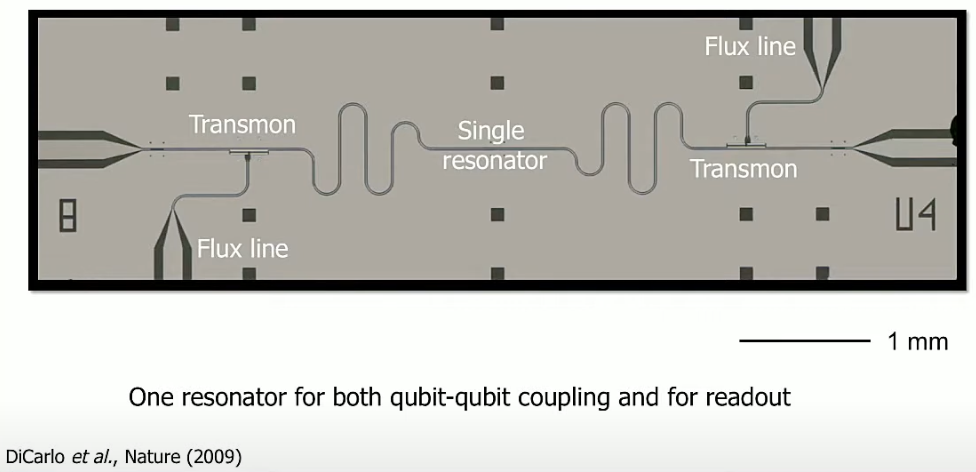
這張圖是兩個量子位元（Transmon）藉由一個 resonator 耦合在一起（間接耦合），可以注意的是下方一行文字寫這個 resonator 兼具耦合兩個量子位元的功能。



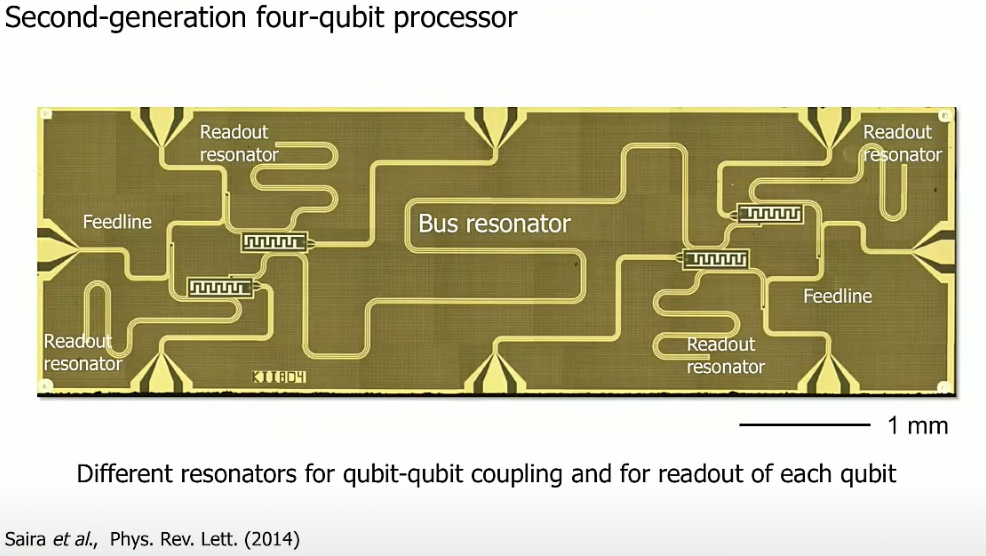
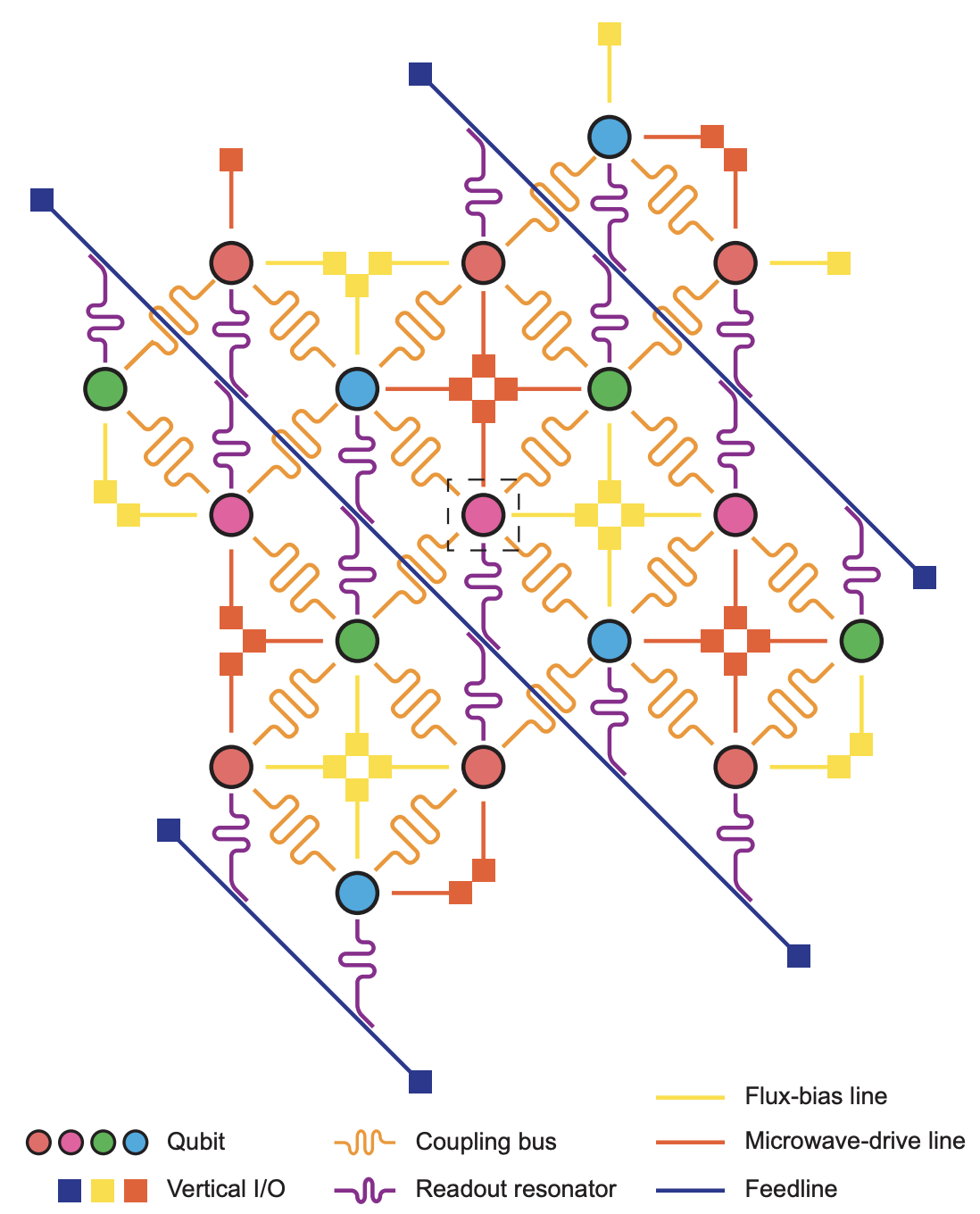
這張圖是四個 Qubit，中間由 bus resonator 串連耦合四個 Qubit。其中四個接頭直通 Qubit，是 flux-\mathcal{L}ine，另外左上跟右下各有一條 readout feedline I/O，各自連結到兩個 readout resonator 並與 Qubit 耦合（等於說一條 readout feedline 會同時讀取兩個 Qubit）。



doi.org/10.1038/nature13171
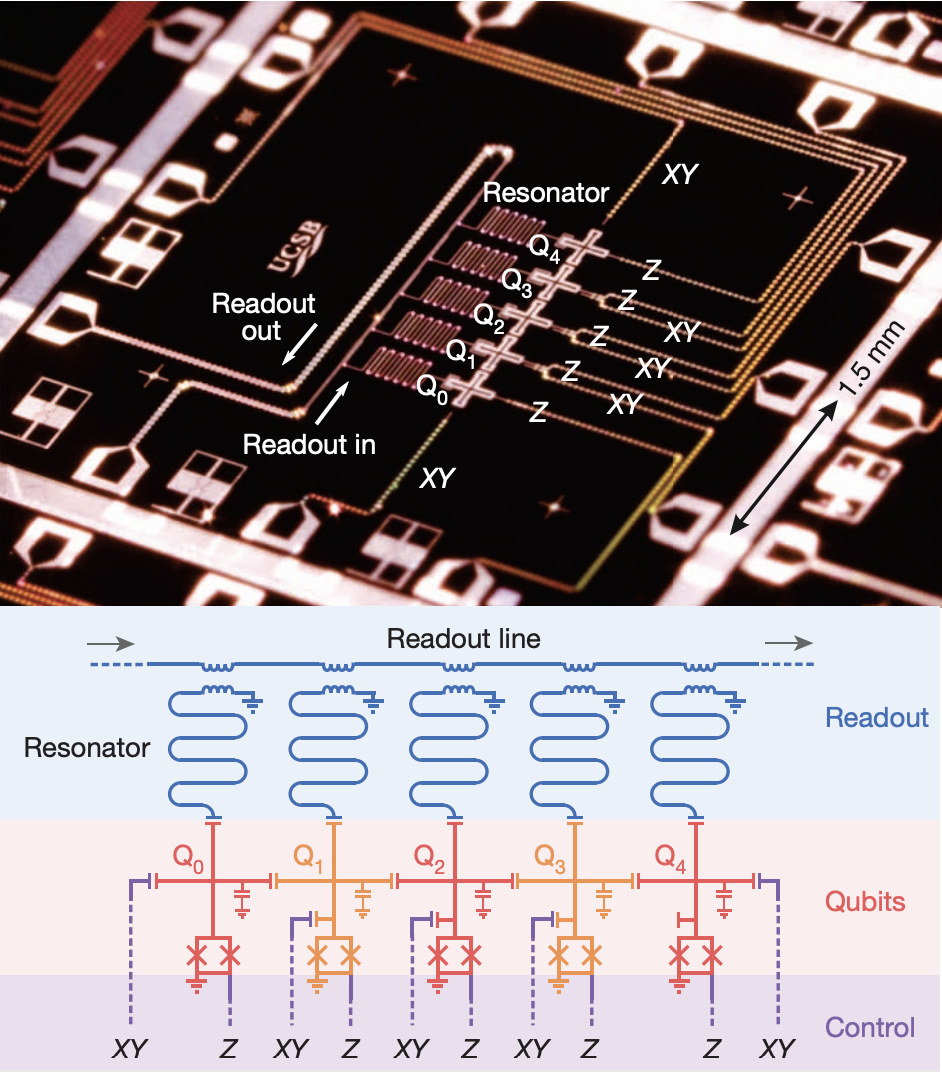
這張是另一種 5 qubit layout 的示意圖。其中 Z 是 flux line，XY 是 Drive line，5 個 Qubit 是直接電容耦合。此外，每個 qubit 都有自己的 readout resonator，在上方併入（此圖顯是是電感耦合）到 readout line。

邁向多 Qubit 模組



https://arxiv.org/pdf/1612.08208
要達到量子計算，需要同時操作許多 Qubit，同時因為糾錯的關係，也需要額外的 Qubit 來進行糾錯。下圖是一個 17 位元的實驗性量子晶片，排列方式是一種稱為 surface code（表面碼）的量子糾錯型態，圓形為 Qubit，粉色及紅色是 Data Qubit，天藍色及綠色是 Check Qubit。每個 Qubit 都連接 7 條線（暱稱為 Starmon），其中 4 條為 Qubit 間耦合、1 條 Flux line、1 條 Drive line、1 條 Readout resonator。Readout resonator 分別併入到三條 feedline。

量子LC電路介紹

量子物理中常見的簡諧震盪，經過量子化後能產生離散的能階，這正是量子計算基礎中的量子位元所依賴的概念。量子位元需要以具有量子效應的元件為基礎，利用超導體作為量子材料，結合 LC 震盪電路的概念，製造出超導量子位元。本節將首先討論 LC 電路的量子化過程。



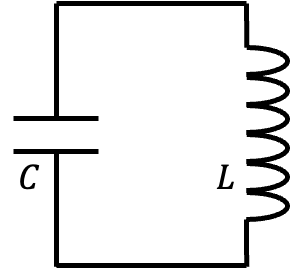
一個基礎的 \(LC\) 震盪電路包含一個電感 \(L\) 和一個電容 \(C\)。定義電容攜帶的電荷為 \(Q\)，當電容儲存的電荷改變速度（即 \(\dot{Q}\)）時，即表示電路上的流動電流。電容和電感分別儲存的能量可表達為： \[ E_C = \frac{Q^2}{2C}, \quad E_L = \frac{L\dot{Q}^2}{2}. \] 我們可以將 \(E_L\) 視為動能項 \(T\)，將 \(E_C\) 視為位能項 \(U\)，從而定義拉格朗日量 \(L\)： \[ \mathcal{L}(\dot{Q}, Q) = T - U = \frac{L\dot{Q}^2}{2} - \frac{Q^2}{2C}. \]

根據歐拉-拉格朗日方程： \[ \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{Q}} - \frac{\partial \mathcal{L}}{\partial Q} = 0, \] 我們得到： \[ L\ddot{Q} + \frac{Q}{C} = 0 \implies \ddot{Q} + \frac{Q}{LC} = 0, \] 即描述一個以頻率 \(\omega = \frac{1}{\sqrt{LC}}\) 震盪的簡諧運動。

LC電路的正則量子化

正則量子化是針對古典系統引入量子結構的一套方法，其核心是將 Hamiltonian 的 Poisson 結構替換為對易關係（commutator relation）。在前一節中，我們已經給出了 Lagrangian，現在透過 Lagendre 變換即可得到 Hamiltonian。

正則動量 \(\Phi_\#\) 定義為： \[ \Phi_\# \equiv \frac{\partial \mathcal{L}}{\partial \dot{Q}} = \mathcal{L}\dot{Q} \leftrightarrow \dot{Q} = \frac{\Phi_\#}{L}. \] 此處 \(\Phi_\#\) 的單位與磁通量相同，可以視為電感內部的磁通量。Hamiltonian \(H(\Phi_\#, Q)\) 定義為： \[ \mathcal{H} \equiv \Phi_\# \dot{Q} - \mathcal{L} = \frac{\Phi_\#^2}{2L} + \frac{Q^2}{2C}. \]

在量子系統中，正則座標 \(q\) 和正則動量 \(p\) 滿足對易關係： \[ [x, p] = i\hbar. \] 對於本文中的參數，量子化條件為： \[ [Q, \Phi_\#] = i\hbar. \]

本文目前採用 \(\Phi_\#\) 作為記號，這是因為與傳統文章採用的方式相反。傳統文章中，Hamiltonian 對於 \(\Phi_\#\) 與 \(Q\) 的地位是對稱的，定義誰是正則座標、誰是正則動量「似乎」是可以對換的（然而，Lagrangian 中動能和位能是反對稱的）。因此，本文直接反過來，將磁通量的部分作為廣義坐標，記為 \(\Phi\)，而 \(Q\) 作為廣義動量。

在這種情況下，量子化條件變為： \[ [\Phi, Q] = i\hbar, \] 與本文的選擇差一個負號，即： \[ \Phi = -\Phi_\#. \] 這個負號也可以由 Lagrangian 的反對稱性進一步解釋。

有一種說法是因為後續會利用非線性的電感元件:約瑟夫森節（Josephson junction）取代線性電感，此非線性項如果出現在位能項比較好理解。不過，後面在驅動量子位元的時候，也是施加電容電壓來驅動，此時卻反而像驅動動能而不是驅動位能。以計算而言，誰是動能誰是位能是沒有差的。

我們引入新的變量 \(a\)、\(a^\dagger\)： \[ a = \sqrt{\frac{1}{2\hbar} \sqrt{\frac{L}{C}}} \left( Q + i\sqrt{\frac{C}{L}} \Phi_\# \right), \quad a^\dagger = \sqrt{\frac{1}{2\hbar} \sqrt{\frac{L}{C}}} \left( Q - i\sqrt{\frac{C}{L}} \Phi_\# \right). \] 反之，可以表示為： \[ Q = \sqrt{\frac{\hbar}{2} \sqrt{\frac{C}{L}}} (a^\dagger + a), \quad \Phi_\# = i\sqrt{\frac{\hbar}{2} \sqrt{\frac{L}{C}}} (a^\dagger - a). \]

易證 \([a, a^\dagger] = 1\)： \[ [a, a^\dagger] = aa^\dagger - a^\dagger a = \frac{1}{2\hbar} \sqrt{\frac{L}{C}} \left[ Q, \Phi_\# \right] = 1. \] 我們可以利用 \(a\)、\(a^\dagger\) 重寫 Hamiltonian \(H(\Phi_\#, Q)\)： \[ \mathcal{H} = \frac{\Phi_\#^2}{2L} + \frac{Q^2}{2C} = \frac{\hbar \omega}{4} \left[ - (a^\dagger - a)^2 + (a^\dagger + a)^2 \right], \] 其中 \(\omega = \frac{1}{\sqrt{LC}}\)。 展開後可得： \[ \mathcal{H} = \frac{\hbar \omega}{2} \left[ a^\dagger a + a^\dagger a + 1 \right] = \hbar \omega \left[ a^\dagger a + \frac{1}{2} \right]. \]

最終得到量子化後的 Hamiltonian，每個能階差為 \(\hbar \omega\)。

動能與位能項的互換

實際上，要正確地透過對易關係（commutator relation）進行量子化，需要嚴格規定 \(x, p\) 的對應關係，否則可能會出現負號上的偏差。承接前一節，我們知道： \[ \dot{\Phi}_\# = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{Q}} = \frac{\partial \mathcal{L}}{\partial Q} = -\frac{Q}{C} \implies Q = -C\dot{\Phi}_\#. \] 現在，我們將 Lagrangian \(L\) 轉換到動量空間。

定義新的 Lagrangian \(\bar{\mathcal{L}}\) 為： \[ \bar{\mathcal{L}} \equiv \mathcal{L} - \frac{d}{dt} (\Phi_\# Q) = \mathcal{L} - \dot{\Phi}_\# Q - \Phi_\# \dot{Q}, \] 展開後可得： \[ \bar{\mathcal{L}} = \frac{L\dot{Q}^2}{2} - \frac{Q^2}{2C} - \dot{\Phi}_\# Q - \Phi_\# \dot{Q} = \frac{\Phi_\#^2}{2L} - \frac{C\dot{\Phi}_\#^2}{2} + C\dot{\Phi}_\#^2 - \frac{\Phi_\#^2}{L}, \] 簡化為： \[ \bar{\mathcal{L}} = \frac{C\dot{\Phi}_\#^2}{2} - \frac{\Phi_\#^2}{2L}. \]

注意，此時 \(\mathcal{L}(Q, \dot{Q}) \to \bar{\mathcal{L}}(\Phi_\#, \dot{\Phi}_\#)\)，動能與位能的角色互換。同時，有 \(\bar{\mathcal{L}} = -\mathcal{L}\)，對應於 Lagrangian 的反對稱性。為吸收這一反對稱性，我們定義新的變量： \[ \Phi = -\Phi_\#. \] 這使得： \[ \bar{\mathcal{L}}(\dot{\Phi}, \Phi) = \frac{C\dot{\Phi}^2}{2} - \frac{\Phi^2}{2L}. \]

對應的正則動量 \(\Pi\)（並利用前述結果與 \(Q\) 進行聯繫）： \[ \Pi \equiv \frac{\partial \bar{\mathcal{L}}}{\partial \dot{\Phi}} = C\dot{\Phi} = -C\dot{\Phi}_\# = Q \implies \dot{\Phi} = \frac{\Pi}{C} = \frac{Q}{C}. \]

Hamiltonian \(\bar{\mathcal{H}}\) 定義為： \[ \bar{\mathcal{H}} = \Pi\dot{\Phi} - \bar{\mathcal{L}} = \frac{\Pi^2}{C} - \frac{\Pi^2}{2C} + \frac{\Phi^2}{2L} = \frac{\Pi^2}{2C} + \frac{\Phi^2}{2L}, \] 與先前的 \(\mathcal{H}\) 完全一致。此時的量子化條件為： \[ [\Phi, \Pi] = [\Phi, Q] = i\hbar, \] 與傳統條件相同。

定義新的變量 \(a\)、\(a^\dagger\)： \[ a = \sqrt{\frac{1}{2\hbar} \sqrt{\frac{L}{C}}} \left( \sqrt{\frac{C}{L}} \Phi + iQ \right), \quad a^\dagger = \sqrt{\frac{1}{2\hbar} \sqrt{\frac{L}{C}}} \left( \sqrt{\frac{C}{L}} \Phi - iQ \right). \] 反之： \[ \Phi = \sqrt{\frac{\hbar}{2} \sqrt{\frac{L}{C}}} (a^\dagger + a), \quad Q = i\sqrt{\frac{\hbar}{2} \sqrt{\frac{C}{L}}} (a^\dagger - a). \]

易證 \([a, a^\dagger] = 1\)： \[ [a, a^\dagger] = aa^\dagger - a^\dagger a = \frac{1}{2\hbar} \sqrt{\frac{L}{C}} \left[ \Phi, Q \right] = 1. \] Hamiltonian \(H(\Phi, Q)\) 可改寫為： \[ \mathcal{H} = \frac{\Phi^2}{2L} + \frac{Q^2}{2C} = \frac{\hbar}{4\sqrt{LC}} \left[ (a^\dagger + a)^2 - (a^\dagger - a)^2 \right]. \] 由於 \(\omega = \frac{1}{\sqrt{LC}}\)，展開後可得： \[ \mathcal{H} = \frac{\hbar \omega}{4} \left[ (a^\dagger + a)^2 - (a^\dagger - a)^2 \right] = \hbar \omega \left[ a^\dagger a + \frac{1}{2} \right]. \]

最終，我們再次得到量子化後的 Hamiltonian，其中每個能階的差異為 \(\hbar \omega\)。

形式化 Lagrangian 動能與位能的互換

從 \(L(\dot{Q}, Q)\) 出發，基於 Lagrangian 動能與位能的反對稱性，我們定義對應 \(\dot{Q}\) 的正則動量 \(\Phi\) 時手動加入一個負號，以吸收反對稱性（否則後續的 Hamiltonian 會為負）： \[ \Phi \equiv -\frac{\partial \mathcal{L}}{\partial \dot{Q}} \implies \dot{\Phi} = -\frac{\partial \mathcal{L}}{\partial Q}. \] 接下來，我們將 Lagrangian 換到 \((\dot{\Phi}, \Phi)\) 空間，即動量空間的 Lagrangian \(\bar{\mathcal{L}}\)： \[ \bar{\mathcal{L}} \equiv \mathcal{L} + \frac{d}{dt} (\Phi Q) = \mathcal{L} + \dot{\Phi} Q + \Phi \dot{Q}. \]

利用微分的方式，可以證明 \(\bar{\mathcal{L}} = \bar{\mathcal{L}}(\dot{\Phi}, \Phi)\) 是 \((\dot{\Phi}, \Phi)\) 空間的函數： \[ d\bar{\mathcal{L}} = d\mathcal{L} + d(\dot{\Phi} Q) + d(\Phi \dot{Q}) = \frac{\partial \mathcal{L}}{\partial \dot{Q}} d\dot{Q} + \frac{\partial \mathcal{L}}{\partial Q} dQ + Qd\dot{\Phi} + \dot{\Phi}dQ + \dot{Q}d\Phi + \Phi d\dot{Q}. \] 展開後，因為 \(-\Phi = \frac{\partial \mathcal{L}}{\partial \dot{Q}}\)，我們有： \[ d\bar{\mathcal{L}} = -\Phi d\dot{Q} - \dot{\Phi} dQ + Q d\dot{\Phi} + \dot{\Phi} dQ + \dot{Q} d\Phi + \Phi d\dot{Q} = Q d\dot{\Phi} + \dot{Q} d\Phi. \]

此時，對應 \(\dot{\Phi}\) 的正則動量 \(\Pi\) 為： \[ \Pi = \frac{\partial \bar{\mathcal{L}}}{\partial \dot{\Phi}} = Q, \] 即與原來的 \(Q\) 相同。對應的 Hamiltonian \(\bar{\mathcal{H}}\) 定義為： \[ \bar{\mathcal{H}} = \Pi \dot{\Phi} - \bar{\mathcal{L}} = Q\dot{\Phi} - \mathcal{L} - \dot{\Phi} Q - \Phi \dot{Q} = -\mathcal{L} - \Phi \dot{Q}. \] 最終形式為： \[ \bar{\mathcal{H}}(Q, \Phi) = -\mathcal{L} - \Phi \dot{Q}. \]

這樣，我們可以簡化後續的推導，只需遵循以下步驟：

1. 寫下 \(L(\dot{Q}, Q)\)。
2. 定義 \(\Phi \equiv -\frac{\partial \mathcal{L}}{\partial \dot{Q}}\)，並得到 \(\dot{Q}\) 與 \(\Phi\) 的關係。
3. 直接求出對應的 Hamiltonian： \[ \bar{\mathcal{H}}(Q, \Phi) = -\mathcal{L} - \Phi \dot{Q}, \] 並將 \(\dot{Q}\) 代入前述關係式。
4. 量子化條件： \[ [Q, \Phi] = i\hbar. \]

這樣無需經過繁瑣的轉換 \(L(\dot{Q}, Q) \to \bar{\mathcal{L}}(\dot{\Phi}, \Phi) \to \bar{\mathcal{H}}(Q, \Phi)\)。特別是在後續引入外力耦合項時（如在推導如何驅動與讀取量子位元時，外部訊號與量子位元交互作用，或是兩個量子位元之間的耦合），如果按照繁瑣的推導，會出現類似於電磁場下的動量 \(p \to p - eA\) 的情況，在中間轉換時極度複雜。

註：注意到： \[ \bar{\mathcal{H}}(Q, \Phi) = -\mathcal{L} - \Phi \dot{Q} = -\mathcal{L} + \frac{\partial \mathcal{L}}{\partial \dot{Q}} \dot{Q} = H(\Phi, Q). \] \(H(\Phi, Q)\) 就是傳統上熟悉的 Hamiltonian。同時，\(\bar{\mathcal{H}} = H\) 再一次表明了 Hamiltonian 動能與位能的對稱性。

約瑟夫森節的非線性電感性質



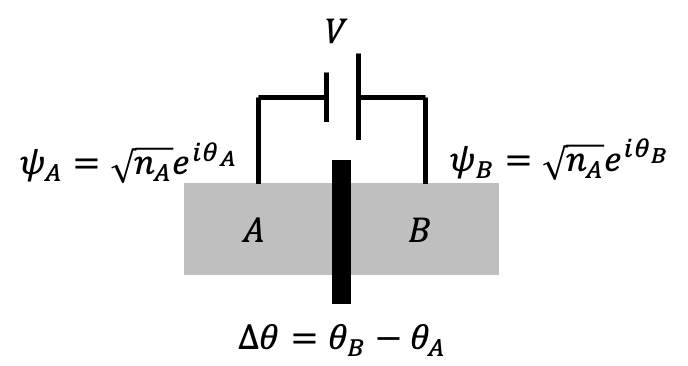
描述一個約瑟夫森接面，其材料的內秉性質由 \(H_0\) 描述。在接面兩端施加電壓 \(V\)，超導波函數之間的交互作用以 \(K\) 表示，其運動方程為： \[ i\hbar \frac{\partial}{\partial t} \begin{pmatrix} \sqrt{n_A} e^{i\theta_A} \\ \sqrt{n_B} e^{i\theta_B} \end{pmatrix} = \begin{pmatrix} H_0 - \frac{qV}{2} & K \\ K & H_0 + \frac{qV}{2} \end{pmatrix} \begin{pmatrix} \sqrt{n_A} e^{i\theta_A} \\ \sqrt{n_B} e^{i\theta_B} \end{pmatrix}. \] 當 \(q = -2e\)（古柏對）時，方程變為： \[ i\hbar \frac{\partial}{\partial t} \begin{pmatrix} \sqrt{n_A} e^{i\theta_A} \\ \sqrt{n_B} e^{i\theta_B} \end{pmatrix} = \begin{pmatrix} H_0 + eV & K \\ K & H_0 - eV \end{pmatrix} \begin{pmatrix} \sqrt{n_A} e^{i\theta_A} \\ \sqrt{n_B} e^{i\theta_B} \end{pmatrix}. \]

\(\theta_A, n_A \)完整推導過程

第一條方程為： \[ i\hbar \frac{\partial}{\partial t} (\sqrt{n_A} e^{i\theta_A}) = \frac{i}{2} \frac{e^{i\theta_A}}{\sqrt{n_A}} \frac{\partial n_A}{\partial t} - \sqrt{n_A} e^{i\theta_A} \frac{\partial \theta_A}{\partial t} = (H_0 + eV) \sqrt{n_A} e^{i\theta_A} + K\sqrt{n_B} e^{i\theta_B}. \] 將實部與虛部分離後得到： \[ \frac{i}{2}\hbar \frac{\partial n_A}{\partial t} - n_A \hbar \frac{\partial \theta_A}{\partial t} = (H_0 + eV)n_A + K\sqrt{n_A n_B} e^{i(\theta_B - \theta_A)}. \] 其共軛方程為： \[ -\frac{i}{2}\hbar \frac{\partial n_A}{\partial t} - n_A \hbar \frac{\partial \theta_A}{\partial t} = (H_0 + eV)n_A + K\sqrt{n_A n_B} e^{-i(\theta_B - \theta_A)}. \]

將兩式相加可得： \[ -2n_A \hbar \frac{\partial \theta_A}{\partial t} = 2(H_0 + eV)n_A + 2K\sqrt{n_A n_B} \cos(\theta_B - \theta_A), \] 整理得到 \(\theta_A\) 的方程： \[ \hbar \frac{\partial \theta_A}{\partial t} = -(H_0 + eV) - K\sqrt{\frac{n_B}{n_A}} \cos(\theta_B - \theta_A). \]
將兩式相減可得： \[ i\hbar \frac{\partial n_A}{\partial t} = 2iK\sqrt{n_A n_B} \sin(\theta_B - \theta_A), \] 即： \[ \hbar \frac{\partial n_A}{\partial t} = 2K\sqrt{n_A n_B} \sin(\theta_B - \theta_A). \]

\(\theta_B, n_B \)完整推導過程

第二條方程為： \[ i\hbar \frac{\partial}{\partial t} (\sqrt{n_B} e^{i\theta_B}) = \frac{i}{2} \frac{e^{i\theta_B}}{\sqrt{n_B}} \frac{\partial n_B}{\partial t} - \sqrt{n_B} e^{i\theta_B} \frac{\partial \theta_B}{\partial t} = K\sqrt{n_A} e^{i\theta_A} + (H_0 - eV)\sqrt{n_B} e^{i\theta_B}. \] 拆分後為： \[ \frac{i}{2}\hbar \frac{\partial n_B}{\partial t} - n_B \hbar \frac{\partial \theta_B}{\partial t} = K\sqrt{n_A n_B} e^{-i(\theta_B - \theta_A)} + (H_0 - eV)n_B. \] 其共軛方程為： \[ -\frac{i}{2}\hbar \frac{\partial n_B}{\partial t} - n_B \hbar \frac{\partial \theta_B}{\partial t} = K\sqrt{n_A n_B} e^{i(\theta_B - \theta_A)} + (H_0 - eV)n_B. \]

將兩式相加可得： \[ -2n_B \hbar \frac{\partial \theta_B}{\partial t} = 2K\sqrt{n_A n_B} \cos(\theta_B - \theta_A) + 2(H_0 - eV)n_B, \] 整理得到 \(\theta_B\) 的方程： \[ \hbar \frac{\partial \theta_B}{\partial t} = -(H_0 - eV) - K\sqrt{\frac{n_A}{n_B}} \cos(\theta_B - \theta_A). \]
將兩式相減可得： \[ i\hbar \frac{\partial n_B}{\partial t} = -2iK\sqrt{n_A n_B} \sin(\theta_B - \theta_A), \] 即： \[ \hbar \frac{\partial n_B}{\partial t} = -2K\sqrt{n_A n_B} \sin(\theta_B - \theta_A). \]

整理得出以下方程：

• 對於 \(\theta_A\)： \[ \hbar \frac{\partial \theta_A}{\partial t} = -(H_0 + eV) - K\sqrt{\frac{n_B}{n_A}} \cos(\theta_B - \theta_A). \]
• 對於 \(\theta_B\)： \[ \hbar \frac{\partial \theta_B}{\partial t} = -(H_0 - eV) - K\sqrt{\frac{n_A}{n_B}} \cos(\theta_B - \theta_A). \]
• 對於 \(n_A\)： \[ \hbar \frac{\partial n_A}{\partial t} = 2K\sqrt{n_A n_B} \sin(\theta_B - \theta_A). \]
• 對於 \(n_B\)： \[ \hbar \frac{\partial n_B}{\partial t} = -2K\sqrt{n_A n_B} \sin(\theta_B - \theta_A). \]

定義相位差 \(\Delta \theta = \theta_B - \theta_A\)，並將前兩個方程相減，可得： \[ \hbar \frac{\partial \Delta \theta}{\partial t} = 2eV + \frac{K}{\hbar} \left( \frac{n_B - n_A}{\sqrt{n_A n_B}} \right) \cos\Delta \theta. \] 將後兩條方程結合並定義電流 \(I\) 為： \[ -\frac{\partial n_A}{\partial t} = \frac{\partial n_B}{\partial t} \equiv \frac{I}{-2e}. \] 整理得到： \[ I = \frac{4eK}{\hbar} \sqrt{n_A n_B} \sin\Delta \theta \equiv I_c \sin\Delta \theta, \] 其中 \(I_c\) 為該約瑟夫森接面的臨界電流。

定義約瑟夫森接面的非線性電感： \[ L_J(\Delta \theta) = \left(\frac{2e}{\hbar I_c \cos\Delta \theta}\right). \] 電感儲存的能量為： \[ E = \int IV dt = \int I_0 \sin\Delta \theta \cdot \frac{\hbar}{q} \frac{\partial \Delta \theta}{\partial t} dt = -\frac{I_0 \hbar}{2e} \cos\Delta \theta \equiv -\frac{I_0 \Phi_0}{2\pi} \cos\Delta \theta, \] 其中，磁通量子 \(\Phi_0 = \frac{2\pi\hbar}{2e}\)，並定義： \[ E_J = \frac{I_0 \Phi_0}{2\pi}. \]



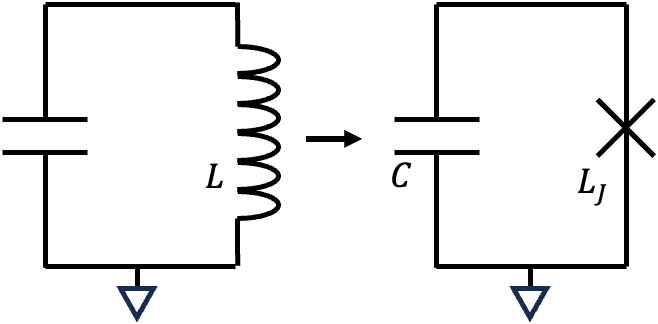
▲從線性的\(LC\)電路，變成以約瑟夫森節的非線性電感組合出的非線性\(LC\)電路。\(L_J\)為約瑟夫森節的電感值。

雙約瑟夫森節（SQUID）的非線性電感性質



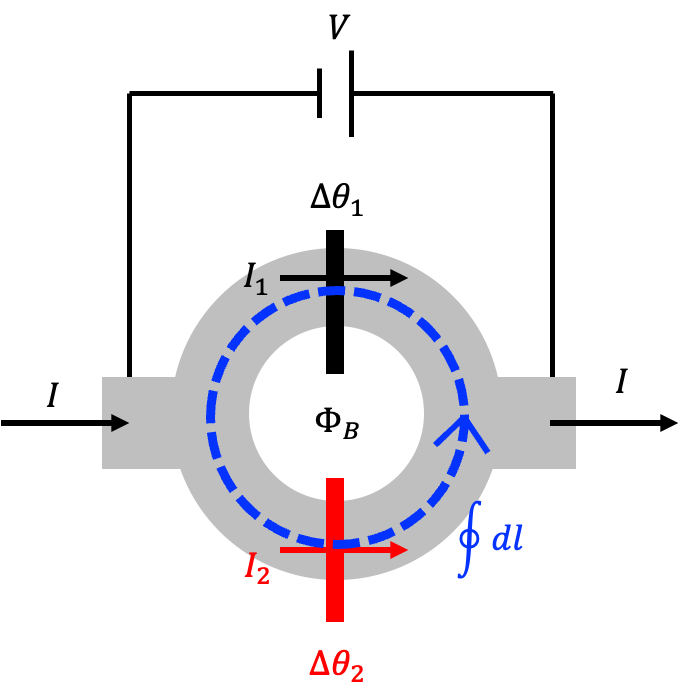
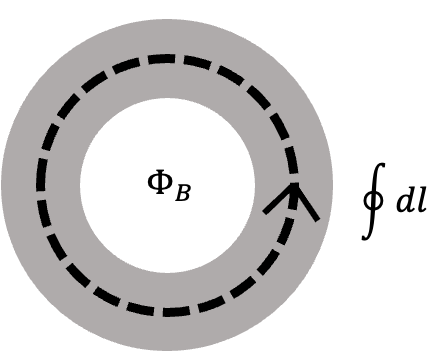
將兩組約瑟夫森節 \(J_1\)、\(J_2\) 相組，中間形成一個閉環，通入磁通 \( \Phi_B \) 與電壓 \( V \)。在前一節中，超導函數的相位對閉環的積分需滿足： \[ \oint \nabla \theta(r) \cdot d\vec{l} - \frac{q}{\hbar} \Phi_B = 2\pi N \] 因為在接面不連續會貢獻 \( \Delta\theta_1 \)、\( \Delta\theta_2 \)，\( q = -2e \)，帶入得： \[ \Delta\theta_2 - \Delta\theta_1 + 2\pi \frac{\Phi_B}{\Phi_0} = 2\pi N \] \[ \Delta\theta_2 = \Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0} + 2\pi N \]

當整個 SQUID 通入電流 \( I = I_1 + I_2 \)，並使用前一節約瑟夫森節電流的關係式（這裡考慮對稱的 SQUID，即兩個約瑟夫森節的特性 \( I_c \) 相同），計算得： \[ I = I_1 + I_2 = I_0 (\sin\Delta\theta_1 + \sin\Delta\theta_2) \] \[ I = I_0 \left[\sin\Delta\theta_1 + \sin\left(\Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0} + 2\pi N\right)\right] \] \[ I = I_0 \left[\sin\Delta\theta_1 + \sin\left(\Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0}\right)\right] \] 利用三角恆等式化簡： \[ I = I_0 \left[2 \sin\left(\frac{\Delta\theta_1 + \Delta\theta_1 - 2\pi \frac{\Phi_B}{\Phi_0}}{2}\right) \cos\left(\frac{\Delta\theta_1 - \Delta\theta_1 + 2\pi \frac{\Phi_B}{\Phi_0}}{2}\right)\right] \] \[ I = 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \sin\left(\Delta\theta_1 - \frac{\Phi_B}{\Phi_0} \pi\right) \]

前一節提到約瑟夫森節具有電感的性質，同理我們可以討論 SQUID 的電感性質。將電流對時間微分： \[ \dot{I} = 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \cos\left(\Delta\theta_1 - \frac{\Phi_B}{\Phi_0} \pi\right) \dot{\Delta\theta_1} \] 而 \( \dot{\Delta\theta_1} \) 與電壓 \( V \) 的關係為： \[ V = \frac{\hbar}{2e} \dot{\Delta\theta_1} = \frac{\Phi_0}{2\pi} \dot{\Delta\theta_1} \] 帶入後可得電感值： \[ L_{\text{SQUID}}(\Delta\theta_1, \Phi_B) = \left[\frac{2\pi}{\Phi_0} \cdot 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \cos\left(\Delta\theta_1 - \frac{\Phi_B}{\Phi_0} \pi\right)\right] \]

可以注意到 \( L_{\text{SQUID}} \) 的值會受到外加磁通 \( \Phi_B \) 的影響，這為後來 Tunable Transmon 調整頻率的關鍵。定義變數 \( \Phi \)： \[ \Phi \equiv \frac{\Delta\theta_1}{\pi} \Phi_0 - \Phi_B = \frac{\Phi_0}{\pi} \left(\Delta\theta_1 - \frac{\Phi}{\Phi_0} \pi\right) \] 並有： \[ \dot{\Phi} = \frac{\Phi_0}{\pi} \dot{\Delta\theta_1} \] 電壓 \( V \) 和電流 \( I \) 分別為： \[ V = \frac{1}{2} \dot{\Phi}, \quad I = 2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \sin\left(\frac{\Phi}{\Phi_0} \pi\right) \]

固定外場 \( \Phi_B \) 下，一組 SQUID 儲存的能量為： \[ E = \int IV \, dt = \int \left[2I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \sin\left(\frac{\Phi}{\Phi_0} \pi\right) \cdot \frac{1}{2} \dot{\Phi}\right] dt \] 化簡得： \[ E = I_0 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \int \sin\left(\frac{\Phi}{\Phi_0} \pi\right) d\Phi \] \[ E = -\frac{I_0 \Phi_0}{\pi} \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \cos\left(\frac{\pi}{\Phi_0} \Phi\right) \]



▲由兩個約瑟夫森節組合成可調電感值的\(LC\)電路。

Transmon的性質



Ref: DOI:10.48550/arXiv.2203.04164

前文提及約瑟夫森節具有電感性質，Transmon即是LC電路中的電感替換成約瑟夫森節。本節直接討論 Tunable Transmon，採用 SQUID 當作電感。實務上因為材料製作的不均一性，不同 Transmon 會有不一樣的特性，如果採用 Tunable Transmon，可以透過微調磁通量 \( \Phi_B \) 的方式使 Qubit 性質一致。此外，我們在前面量子化 LC 電路時，\([ \Phi, Q ] = i\hbar\) 是一對正則變量，利用 SQUID 的推導可以很自然地將磁通量 \( \Phi \) 與相位差 \( \Delta\theta \) 做聯繫，即： \[ \Phi \equiv \frac{\Delta\theta_1}{\pi} \Phi_0 - \Phi_B \]

現在我們寫下 Hamiltonian： \[ \mathcal{H} = \frac{Q^2}{2C} + \frac{\Phi_\#^2}{2L} = \frac{Q^2}{2C} + \frac{(I_0 \pi)}{2\Phi_0} \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \Phi^2 - \frac{I_0}{24} \left(\frac{\pi}{\Phi_0}\right)^3 \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right) \Phi^4 + \cdots \] \[ = \frac{Q^2}{2C} + \frac{\Phi^2}{2L} - \frac{1}{24L} \left(\frac{\pi}{\Phi_0}\right)^2 \Phi^4 + \cdots \] 其中： \[ L = \left(\frac{I_0 \pi}{\Phi_0} \cos\left(\frac{\Phi_B}{\Phi_0} \pi\right)\right)^{-1} \]

現在我們要討論非線性對於能階的改變，前文我們選擇新的變量 \( a \)、\( a^\dagger \)： \[ a = \sqrt{\frac{1}{2\hbar} \sqrt{ \frac{L}{C}}} \left(\sqrt{\frac{C}{L}} \Phi + iQ\right), \quad a^\dagger = \sqrt{\frac{1}{2\hbar} \sqrt{ \frac{L}{C}}} \left(\sqrt{\frac{C}{L}} \Phi - iQ\right) \] 反之： \[ \Phi = \sqrt{\frac{\hbar}{2 }\sqrt{ \frac{L}{C}}} (a^\dagger + a), \quad Q = i\sqrt{\frac{\hbar}{2} \sqrt{ \frac{C}{L}}} (a^\dagger - a) \]

將 Hamiltonian 表達式展開為： \[ \mathcal{H} = \frac{\hbar}{\sqrt{LC}} \left[a^\dagger a + \frac{1}{2}\right] - \frac{1}{24L} \left(\frac{\pi}{\Phi_0}\right)^2 \left[i \sqrt{\frac{\hbar}{2\sqrt{L/C}}} (a^\dagger + a)\right]^4 \] 化簡後： \[ \mathcal{H} = \frac{\hbar}{\sqrt{LC}} \left[a^\dagger a + \frac{1}{2}\right] - \frac{\hbar^2}{96C} \left(\frac{\pi}{\Phi_0}\right)^2 (a^\dagger + a)^4 \] 該表達式包含線性和非線性項，線性項描述的是量子簡諧振子的能階，而非線性項源自於 Josephson 節對於能階的修正。

利用微擾理論，當 \( \mathcal{H} = H_0 + \Delta H \)， \( |E_0^m\rangle \to |E^m\rangle \)、 \( E_0^m \to E^m = E_0^m + \delta E^m \)，我們知道對能階 \( E_0^m \) 的修正 \( \delta E^m \) 為：

\[ \delta E^m = \langle E_0^m | \Delta H | E_0^m \rangle = \langle E_0^m | \left[-\frac{\hbar^2}{96C} \left(\frac{\pi}{\Phi_0}\right)^2 (a^\dagger + a)^4\right] | E_0^m \rangle \]

計算如下：

\[ \langle E_0^m | (a^\dagger + a)^4 | E_0^m \rangle = \langle E_0^m | (aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger)^2 | E_0^m \rangle \]

展開為：

\[ \langle E_0^m | aa(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) + aa^\dagger(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) + a^\dagger a(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) + a^\dagger a^\dagger(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) | E_0^m \rangle \]

因為取期望值，只會留下 \( a, a^\dagger \) 次數相等的項，剩下：

\[ \langle E_0^m | aaa^\dagger a^\dagger + aa^\dagger aa^\dagger + aa^\dagger a^\dagger a + a^\dagger aaa^\dagger + a^\dagger aa^\dagger a + a^\dagger a^\dagger aa | E_0^m \rangle \]

繼續簡化：

\[ \langle E_0^m | a(a^\dagger a + 1)a^\dagger + aa^\dagger aa^\dagger + (a^\dagger a + 1)a^\dagger a + a^\dagger a(a^\dagger a + 1) + a^\dagger aa^\dagger a + a^\dagger (aa^\dagger - 1)a | E_0^m \rangle \]

再整理為：

\[ \langle E_0^m | aa^\dagger aa^\dagger + aa^\dagger + aa^\dagger aa^\dagger + a^\dagger aa^\dagger a + a^\dagger a + a^\dagger aa^\dagger a + a^\dagger a + a^\dagger aa^\dagger a + a^\dagger aa^\dagger a - a^\dagger a | E_0^m \rangle \]

進一步簡化：

\[ \langle E_0^m | 2aa^\dagger aa^\dagger + aa^\dagger + 4a^\dagger aa^\dagger a + a^\dagger a | E_0^m \rangle \] \[ = \langle E_0^m | 2(a^\dagger a + 1)(a^\dagger a + 1) + (a^\dagger a + 1) + 4a^\dagger aa^\dagger a + a^\dagger a | E_0^m \rangle \]

最終得到：

\[ \langle E_0^m | 6a^\dagger aa^\dagger a + 6a^\dagger a + 3 | E_0^m \rangle = 6m^2 + 6m + 3 \]

定義能階差：

\[ \Delta E^m_{m-1} = \frac{\hbar}{\sqrt{LC}} - \frac{\hbar^2}{96C} \left(\frac{\pi}{\Phi_0}\right)^2 \left\{6[m^2 - (m-1)^2] + 6\right\} \]

\[ = \frac{\hbar}{\sqrt{LC}} - \frac{\hbar^2 \pi^2}{96C} \frac{e^2}{\pi^2 \hbar^2} \left[6(2m - 1) + 6\right] \]

最終得到：

\[ \Delta E^m_{m-1} = \frac{\hbar}{\sqrt{LC}} - m\frac{e^2}{8C} \]

計算 \( \Delta E^{21} - \Delta E^{10} \)：

\[ \Delta E^{21} - \Delta E^{10} = \left(\frac{\hbar}{\sqrt{LC}} - 2\frac{e^2}{8C}\right) - \left(\frac{\hbar}{\sqrt{LC}} - \frac{e^2}{8C}\right) \]

\[ = -\frac{e^2}{8C} \equiv -E_C \]

\( E_C \) 表示其非線性效應。



Ref: DOI:10.1103/RevModPhys.93.025005

計算科學與二階系統（TLS）

現代電腦運作的原理利用位元進行資訊的儲存、邏輯閘進行運算。資訊會以二進制的編碼表示成0與1的代碼，再將一系列位元依指定的方式變成0或1的狀態，來儲存資訊。例如說，想要儲存19這個數字資訊，換算成二進制表示為10011，這時候可以如果記憶體為八個位元做存儲：

\[ \ket{bit_1} \ket{bit_2} \ket{bit_3} \ket{bit_4} \ket{bit_5} \ket{bit_6} \ket{bit_7} \ket{bit_8} \] 狀態改變成： \[ \ket{0} \ket{0} \ket{0} \ket{1} \ket{0} \ket{0} \ket{1} \ket{1} \]

在量子簡諧振子中，不同能階 \( n \)，可以用 \( a^\dagger \) 和 \( a \) 來聯繫：

\[ \ket{n+1} = \frac{a^\dagger}{ \sqrt{n+1}} \ket{n}, \quad \ket{n-1} = \frac{a}{ \sqrt{n} }\ket{n}, \quad \ket{n} = \frac{(a^\dagger)^n}{\sqrt{n!}} \ket{0} \]

在此情況下：

\[ a^\dagger = \left(\begin{matrix} 0 &1 & 0 & \cdots \\ 0 & 0 & \sqrt{2} & \cdots \\ 0 & 0 & 0 & \cdots \\ \vdots & \vdots & \vdots & \ddots \\ \end{matrix}\right) \]

\[ a = \left(\begin{matrix} 0 & 0 & 0 & \cdots \\ 1 & 0 & 0 & \cdots \\ 0 & \sqrt{2} & 0 & \cdots \\ \vdots & \vdots & \vdots & \ddots \\ \end{matrix}\right) \]

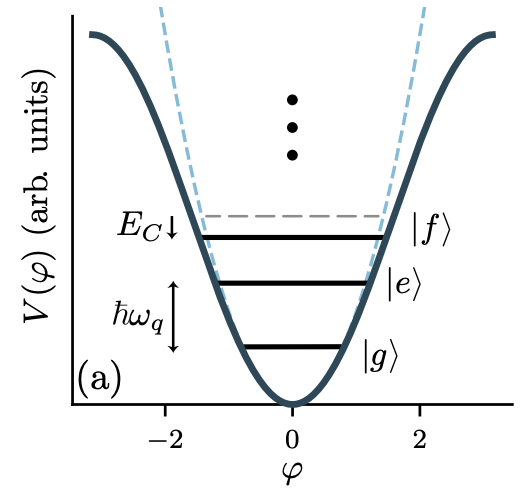
這是一個無窮維的量子系統。一個超導量子位元是取 Transmon 的基態 \( \ket{0} \)（或 \( \ket{g} \)）與第一激發態 \( \ket{1} \)（或 \( \ket{e} \)）作為運算單元。在量子計算的二維框架下：

\[ a^\dagger \rightarrow \sigma^+ = \begin{bmatrix} 0 & 1 \\ 0 & 0 \\ \end{bmatrix}, \quad a \rightarrow \sigma^- = \begin{bmatrix} 0 & 0 \\ 1 & 0 \\ \end{bmatrix} \]

此時可以定義：

\[ \sigma_x = \sigma^+ + \sigma^- = \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix}, \quad \sigma_y = i \left(\sigma^+ - \sigma^- \right)= \begin{bmatrix} 0 & -i \\ i & 0 \\ \end{bmatrix}, \quad \sigma_z = \mathbb{I} - 2\sigma^+\sigma^- = \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} \]

即是大名鼎鼎的包立矩陣。這邊有一些代數結構：

\[ \{\sigma^-, \sigma^+\} = \sigma^-\sigma^+ + \sigma^+\sigma^- = \mathbb{I} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}, \quad [\sigma^-, \sigma^+] = \sigma^-\sigma^+ - \sigma^+\sigma^- = \sigma_z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} \]

對於 \( i, j, k = x, y, z \)：

\[ \sigma_i \sigma_j = \delta_{ij}\mathbb{I} + i\epsilon_{ijk}\sigma_k \]

包立矩陣與三維空間的旋轉高度相關。但讀者也許想問，為何二維的位元系統會出現三維旋轉呢？下一節將討論所謂的量子位元與布洛赫球表示。

量子位元與布洛赫球表示

布洛赫球是一個用來幾何化描述量子位元狀態的工具。在二維量子位元系統中，任何量子態都可以表示為基態 \( \ket{0} \) 和激發態 \( \ket{1} \) 的線性組合：

\[ \ket{\psi} = \alpha \ket{0} + \beta \ket{1}, \] 其中 \( \alpha, \beta \) 為複數，滿足正規化條件 \( |\alpha|^2 + |\beta|^2 = 1 \)。

若將 \( \alpha \) 和 \( \beta \) 表示為球坐標系中的參數，我們可以寫成：

\[ \ket{\psi} = \cos\left(\frac{\theta}{2}\right)\ket{0} + e^{i\phi}\sin\left(\frac{\theta}{2}\right)\ket{1}, \] 其中 \( \theta \) 是 \( z \)-軸與量子態向量的夾角，\( \phi \) 是 \( x \)-\( y \) 平面內的相位角。

這個表示法使得量子位元的狀態可以被視為一個位於半徑為1的三維球面上的點，這就是布洛赫球。布洛赫球上的特殊點包括：

• 北極 (\( \theta = 0 \)): 對應 \( \ket{0} \)
• 南極 (\( \theta = \pi \)): 對應 \( \ket{1} \)
• 赤道 (\( \theta = \pi/2 \)): 對應等幅超位置態，例如 \( \frac{1}{\sqrt{2}}(\ket{0} + e^{i\phi}\ket{1}) \)

布洛赫球的三個坐標軸對應於包立矩陣的期望值：

\[ x = \langle \sigma_x \rangle, \quad y = \langle \sigma_y \rangle, \quad z = \langle \sigma_z \rangle, \] 其中： \[ \langle \sigma_x \rangle = 2\text{Re}(\alpha^*\beta), \quad \langle \sigma_y \rangle = 2\text{Im}(\alpha^*\beta), \quad \langle \sigma_z \rangle = |\alpha|^2 - |\beta|^2. \]

透過布洛赫球表示，我們可以直觀地觀察量子位元的狀態演化。例如，若量子位元受到一個旋轉操作 \( R_x(\theta) = e^{-i\theta \sigma_x / 2} \)，其狀態會沿著 \( x \)-軸旋轉角度 \( \theta \)。這種幾何化描述對量子計算的控制與觀測提供了極大的便利。

布洛赫球不僅是描述單個量子位元的工具，也是理解量子門操作、量子糾纏以及相干性的基石。在後續內容中，我們將進一步探討如何利用布洛赫球來進行量子計算的設計與模擬。

驅動 LC 電路



現在我們來討論如何驅動 LC 電路與 Transmon。透過耦合電容 \( C_d \) 與外部電壓源 \( V_d \) 耦合，系統的 Lagrangian 為：

\[ \mathcal{L}_d(\dot{Q}, Q) = T - U = \frac{L\dot{Q}^2}{2} - \frac{Q^2}{2C} - \frac{Q_d^2}{2C_d} \]

其中耦合電容 \( C_d \) 所攜帶的能量為：

\[ \frac{Q_d^2}{2C_d} = \frac{C_d (V - V_d)^2}{2} = \frac{C_d \left(\frac{Q}{C} - V_d\right)^2}{2} \] \[ = \frac{C_d Q^2}{2C^2} - \frac{C_d Q}{C}V_d + \frac{C_d V_d^2}{2} \]

將上述式子代入並整理得：

\[ \mathcal{L}_d(\dot{Q}, Q) = \frac{L\dot{Q}^2}{2} - \frac{Q^2}{2C} - \frac{C_d}{C} \frac{Q^2}{2C} + \frac{C_d}{C} QV_d - \frac{C_d V_d^2}{2} \] \[ = \frac{L\dot{Q}^2}{2} - \frac{Q^2}{2C_\Sigma} + \frac{C_d}{C} QV_d - \frac{C_d V_d^2}{2} \]

其中 \( C_\Sigma = \frac{C^2}{C + C_d} \)。定義正則動量：

\[ \Phi = -\frac{\partial \mathcal{L}_d}{\partial \dot{Q}} = -L\dot{Q} \quad \rightarrow \quad \dot{Q} = -\frac{\Phi}{L} \]

接著計算 Hamiltonian：

\[ \bar{\mathcal{H}}_d = -\mathcal{L}_d - \Phi \dot{Q}\] \[ = -\frac{L\dot{Q}^2}{2} + \frac{Q^2}{2C_\Sigma} - \frac{C_d}{C} QV_d + \frac{\Phi^2}{L}\] \[ = \frac{\Phi^2}{2L} + \frac{Q^2}{2C_\Sigma} - \frac{C_d}{C} QV_d \]

完整推導過程

接著進行正則量子化：

\[ \begin{aligned} &a_d = \sqrt{\frac{1}{2\hbar} \sqrt{\frac{L}{C_\Sigma}}} \left(\sqrt{\frac{C_\Sigma}{L}} \Phi + iQ\right) \\ &a_d^\dagger = \sqrt{\frac{1}{2\hbar} \sqrt{\frac{L}{C_\Sigma}}} \left(\sqrt{\frac{C_\Sigma}{L}} \Phi - iQ\right) \end{aligned} \] \[\quad \leftrightarrow \quad \begin{aligned} &\Phi_d = \sqrt{\frac{\hbar}{2} \sqrt{\frac{L}{C_\Sigma}}} (a_d^\dagger + a_d) \\ &Q_d = i\sqrt{\frac{\hbar}{2} \sqrt{\frac{C_\Sigma}{L}}} (a_d^\dagger - a_d) \end{aligned} \]

將上述代換代入

\[ =\hbar \sqrt{\frac{1}{LC_\Sigma}} \left( a_d^\dagger a_d + \frac{1}{2} \right) - \frac{C_d}{C} \sqrt{\frac{\hbar}{2 C_\Sigma \sqrt{LC_\Sigma}}} \cdot i (a_d^\dagger - a_d) V_d \]

定義頻率\(\omega_\Sigma = \frac{1}{\sqrt{L C_\Sigma}}\)

\[ = \hbar \omega_\Sigma \left( a_d^\dagger a_d + \frac{1}{2} \right) - C_d V_d \sqrt{\frac{\omega_\Sigma}{2\hbar (C + C_d)}} \cdot i (a_d^\dagger - a_d) \]

最後結果為：

\[ \bar{\mathcal{H}} _d = \hbar \omega_\Sigma \left(a_d^\dagger a_d + \frac{1}{2}\right) - i \Omega (a_d^\dagger - a_d) \]

其中 \( \Omega = C_d V_d \sqrt{\frac{\omega_\Sigma}{2\hbar (C + C_d)}} \) 稱為拉比頻率（Rabi Frequency）。

雙LC電路耦合



要量子計算需要位元之間的耦合，耦合會對量子位元的參數產生影響。可以先討論兩個線性 LC 電路透過電容 \( C_g \) 耦合。

\[ \mathcal{L}_{2LC} = \frac{L_A \dot{Q}_A^2}{2} + \frac{L_B \dot{Q}_B^2}{2} - \frac{Q_A^2}{2C_A} - \frac{Q_B^2}{2C_B} - \frac{Q_g^2}{2C_g} \]

耦合電容 \( C_g \) 的帶電 \( Q_g \) 可以代換為 \( Q_A \) 和 \( Q_B \)，利用電容的性質：

\[ Q_g = C_g (V_A - V_B) = C_g \left( \frac{Q_A}{C_A} - \frac{Q_B}{C_B} \right) \]

將其代入 Lagrangian 並整理得：

\[ \mathcal{L}_{2LC} = \frac{L_A \dot{Q}_A^2}{2} + \frac{L_B \dot{Q}_B^2}{2} - \frac{(C_A + C_g) }{2C_A^2} Q_A^2 - \frac{(C_B + C_g) }{2C_B^2}Q_B^2 + \frac{C_g}{C_A C_B} Q_A Q_B \]

其中定義 \( C_{\Sigma A} = \frac{C_A^2}{C_A + C_g} \)，\( C_{\Sigma B} = \frac{C_B^2}{C_B + C_g} \)。接著定義正則動量：

\[ \Phi_A = -\frac{\partial \mathcal{L}_{2LC}}{\partial \dot{Q}_A} = -L_A \dot{Q}_A \quad \rightarrow \quad \dot{Q}_A = -\frac{\Phi_A}{L_A} \]

計算 Hamiltonian：

\[ \bar{\mathcal{H}}_{2LC} = \frac{\Phi_A^2}{2L_A} + \frac{Q_A^2}{2C_{\Sigma A}} + \frac{\Phi_B^2}{2L_B} + \frac{Q_B^2}{2C_{\Sigma B}} - \frac{C_g}{C_A C_B} Q_A Q_B \]

正則量子化：

\[ \begin{aligned} &a_{\Sigma A} = \sqrt{\frac{1}{2\hbar} \sqrt{\frac{L_A}{C_{\Sigma A}}}} \left(\sqrt{\frac{C_{\Sigma A}}{L_A}} \Phi_A + iQ_A \right) \\ &a_{\Sigma A}^\dagger = \sqrt{\frac{1}{2\hbar} \sqrt{\frac{L_A}{C_{\Sigma A}}}} \left(\sqrt{\frac{C_{\Sigma A}}{L_A}} \Phi_A - iQ_A \right) \end{aligned} \]

定義頻率 \( \omega_{\Sigma A} = \frac{1}{\sqrt{L_A C_{\Sigma A}}} \)，\( \omega_{\Sigma B} = \frac{1}{\sqrt{L_B C_{\Sigma B}}} \)：

\[ \bar{\mathcal{H}}_{2LC} = \hbar \omega_{\Sigma A} \left(a_{\Sigma A}^\dagger a_{\Sigma A} + \frac{1}{2}\right) + \hbar \omega_{\Sigma B} \left(a_{\Sigma B}^\dagger a_{\Sigma B} + \frac{1}{2}\right) - \hbar \Omega_g \, i(a_{\Sigma A}^\dagger - a_{\Sigma A}) \, i(a_{\Sigma B}^\dagger - a_{\Sigma B}) \]

其中，耦合強度 \( \Omega_g \) 定義為：

\[ \Omega_g = C_g \sqrt{\frac{\omega_{\Sigma A}}{2(C_A + C_g)}} \sqrt{\frac{\omega_{\Sigma B}}{2(C_B + C_g)}} \]

附錄：電磁場下薛丁格方程式的機率流

帶電荷 \(q\) 的粒子波函數 \(\Psi\) 滿足薛丁格方程式： \[ i\hbar \partial_t \Psi = \frac{\hat{p}^2}{2m} \Psi + V\Psi, \] 其中動量算符 \(\hat{p}\) 在電磁勢 \((\phi, \mathbf{A})\) 的作用下，表達為（SI 單位）： \[ \hat{p} = \frac{\hbar}{i} \nabla - q\mathbf{A}. \] 將其代入薛丁格方程式，我們得到： \[ i\hbar \partial_t \Psi = \frac{1}{2m} \left( \frac{\hbar}{i} \nabla - q\mathbf{A} \right) \left( \frac{\hbar}{i} \nabla \Psi - q\mathbf{A}\Psi \right) + V\Psi. \] 展開後為： \[ i\hbar \partial_t \Psi = -\frac{\hbar^2}{2m} \nabla^2 \Psi - \frac{q}{2m} \frac{\hbar}{i} \nabla \cdot (\mathbf{A}\Psi) - \frac{q}{2m} \frac{\hbar}{i} \mathbf{A} \cdot \nabla \Psi + \frac{q^2 A^2}{2m} \Psi + \phi\Psi. \]

共軛方程為： \[ -i\hbar \partial_t \Psi^* = -\frac{\hbar^2}{2m} \nabla^2 \Psi^* + \frac{q}{2m} \frac{\hbar}{i} \nabla \cdot (\mathbf{A} \Psi^*) + \frac{q}{2m} \frac{\hbar}{i} \mathbf{A} \cdot \nabla \Psi^* + \frac{q^2 A^2}{2m} \Psi^* + \phi \Psi^*. \]

將兩式分別乘以 \(\Psi^*\) 和 \(\Psi\)，再相減，得到： \[ i\hbar (\Psi^* \partial_t \Psi + \Psi \partial_t \Psi^*) = -\frac{\hbar^2}{2m} (\Psi^* \nabla^2 \Psi - \Psi \nabla^2 \Psi^*) - \frac{q}{2m} \frac{\hbar}{i} \left[ \Psi^* \nabla \cdot (\mathbf{A}\Psi) + \Psi \nabla \cdot (\mathbf{A}\Psi^*) + \Psi^* \mathbf{A} \cdot \nabla \Psi + \Psi \mathbf{A} \cdot \nabla \Psi^* \right]. \] 簡化後得到： \[ i\hbar \partial_t (\Psi^* \Psi) = -\frac{\hbar^2}{2m} \nabla \cdot (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q}{2m} \frac{\hbar}{i} \nabla \cdot (2\mathbf{A} \Psi^* \Psi). \]

除以 \(i\hbar\)，得： \[ \partial_t (\Psi^* \Psi) = -\nabla \cdot \left[ \frac{\hbar}{2mi} (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q\mathbf{A}}{m} \Psi^* \Psi \right]. \] 比較連續性方程式： \[ \partial_t \rho + \nabla \cdot \mathbf{J} = 0, \] 其中 \(\rho = \Psi^* \Psi\) 為機率密度，可得機率流： \[ \mathbf{J} = \frac{\hbar}{2mi} (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q\mathbf{A}}{m} \Psi^* \Psi. \]

對於帶電粒子，其電流密度 \(\mathbf{J}_q\) 為： \[ \mathbf{J}_q = q \mathbf{J} = q \left[ \frac{\hbar}{2mi} (\Psi^* \nabla \Psi - \Psi \nabla \Psi^*) - \frac{q\mathbf{A}}{m} \Psi^* \Psi \right]. \] 若波函數以粒子密度 \(n(\mathbf{r})\) 和相位 \(\theta(\mathbf{r})\) 表示，即 \(\Psi \sim \sqrt{n(\mathbf{r})} e^{i\theta(\mathbf{r})}\)，則有： \[ \mathbf{J}_q = q\frac{\hbar}{m} n(\mathbf{r}) \left[ \nabla \theta(\mathbf{r}) - \frac{q\mathbf{A}}{\hbar} \right]. \]



在拓樸條件下，根據斯托克斯定理： \[ \int \nabla \times \left[ \nabla \theta(\mathbf{r}) - \frac{q\mathbf{A}}{\hbar} \right] \cdot d\mathbf{S} = \int \nabla \times (\nabla \theta(\mathbf{r})) \cdot d\mathbf{S} - \frac{q}{\hbar} \int (\nabla \times \mathbf{A}) \cdot d\mathbf{S}, \] 簡化為： \[ \oint \nabla \theta(\mathbf{r}) \cdot d\mathbf{l} - \frac{q}{\hbar} \Phi_B = \begin{cases} 0, & \text{若環路無孔洞}, \\ 2\pi N, & \text{若環路有孔洞}. \end{cases} \]

附錄：微擾理論下的能階修正計算

利用微擾理論，當 \( \mathcal{H} = H_0 + \Delta H \)， \( |E_0^m\rangle \to |E^m\rangle \)、 \( E_0^m \to E^m = E_0^m + \delta E^m \)，我們知道對能階 \( E_0^m \) 的修正 \( \delta E^m \) 為：

\[ \delta E^m = \langle E_0^m | \Delta H | E_0^m \rangle = \langle E_0^m | \left[-\frac{\hbar^2}{96C} \left(\frac{\pi}{\Phi_0}\right)^2 (a^\dagger + a)^4\right] | E_0^m \rangle \]

完整推導過程

\[ \langle E_0^m | (a^\dagger + a)^4 | E_0^m \rangle = \langle E_0^m | (aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger)^2 | E_0^m \rangle \]

展開為：

\[ \langle E_0^m | aa(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) + aa^\dagger(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) \] \[ + a^\dagger a(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) + a^\dagger a^\dagger(aa + aa^\dagger + a^\dagger a + a^\dagger a^\dagger) | E_0^m \rangle \]

定義能階差：

\[ \Delta E^m_{m-1} = \frac{\hbar}{\sqrt{LC}} - \frac{\hbar^2}{96C} \left(\frac{\pi}{\Phi_0}\right)^2 \left\{6[m^2 - (m-1)^2] + 6\right\} \]

\[ = \frac{\hbar}{\sqrt{LC}} - \frac{\hbar^2 \pi^2}{96C} \frac{e^2}{\pi^2 \hbar^2} \left[6(2m - 1) + 6\right] \]

最終得到：

\[ \Delta E^m_{m-1} = \frac{\hbar}{\sqrt{LC}} - m\frac{e^2}{8C} \]

〈推導〉哈密頓量守恆、變數分離系統

條件:

• 哈密頓量守恆: \(\frac{\partial}{\partial t}H\{|q^{*}|\,|\gamma_{c}|\,t\}=0 \rightarrow H\) function of ... (圖片遮蔽，原應為廣義座標和動量)、 H = E ∈ 運動積分
• 哈密頓特性函數可以分離: \(W(|q^k|, |\alpha_i|) = \sum_k W_k(q^k, |\alpha_i|)\)
• 具有週期性: 可以對於廣義座標定義積分一個週期

考慮哈密頓特性函數作為正則生成函數的正則變換:

\(F_{\alpha\beta}(|q^{*}|,|p_{j}|,t) = F_{2}\{|q^{*}|,||A_{j}|,t\}=W\{|q^{*}|,|\alpha_{i}|\}=\sum_{k}W_{k}(q^{k},|\alpha_{i}|)\)

\(J_n = \oint P_n d q^n\) (不) (目標將其作為新的座標參數)

\(P_n = \frac{\partial}{\partial q^n}W(|q^k|, |\alpha_i|) = \frac{\partial}{\partial q^n}W_n(q^n, |\alpha_i|)\) as function of only \(q^n\). (8)

as function of \(J_n\) ∈ 運動積分

\(J_{n}=\oint_{I}P_{n}(Q^{n}.E)dQ^{n}=\oint_{I}\frac{d}{dq^{n}}W_{n}(q^{n},|\alpha_i|)dQ^{n}\)

直接選取 \(p_n = J_n\)

\(q^n = Q^n = \frac{\partial}{\partial \alpha_n}W(|\alpha_i|) = \frac{\partial}{\partial J_n}W_n(J_n)\)

\(K=H+\frac{\partial W}{\partial t}(|q^k|,|\alpha_i|) = H\) in form of \([|q^n|],[J_n], K=H=E \in\)運動積分

\(\dot{Q}^{a}=\frac{\partial K}{\partial J_{a}}=\frac{\partial K(|\alpha_i|)}{\partial J_{a}}\) (Q.)

\(\dot{J}^{a.}(|\alpha_i|) \in |\alpha_i|\) 運動積分 since \(K = E, J_a \in |\alpha_i|\) 運動積分 \(\rightarrow Q^a(t) = \omega^a J^a (|\alpha_i|)t + Q^a(0)\)

as function of \(J_n\)

\(\dot{Q}^{n}=\frac{d}{dt}J_{n}=\dot{P}_{n}=-\frac{\partial K}{\partial Q^{n}}\rightarrow K\)

-----------------

〈推導〉哈密頓量守恆・變數分離系統

條件：

• 哈密頓量守恆：
\[ \frac{\partial H}{\partial t} (\Psi^1, \Psi^2, t) = 0 \Rightarrow H \text{ as function of } |\Psi^1|, |\Psi^2| \] \[ H = E \in \text{運動積分} \]
• 哈密頓特性函數變數可以分離：
\[ W(\Psi^1, \Psi^2, t) = \sum W_{\lambda}(\Psi^1, \Psi^2) \]
• 具有週期解：可以將座標變數拆解為一個周期

考慮哈密頓特性函數作為正則生成函數的正則變換：

\[ F_1(q^*, p^*, t) = F_1(q^*, J_{\alpha}, t) = W(q^*, J_{\alpha}) = \sum W_{\lambda}(q^*, J_{\alpha}) \] \[ J_{\alpha} = \oint p_{\alpha} dq^* \quad \text{(不失一般性, 目標將其作為新的座標變數)} \] \[ p_{\alpha} = \frac{\partial F_1}{\partial q^*} = \frac{\partial}{\partial q^*} \sum W_{\lambda}(q^*, J_{\alpha}) = \frac{\partial}{\partial q^*} W_{\lambda}(q^*, J_{\alpha}) \] \[ J_{\alpha} = \oint \frac{\partial}{\partial q^*} W_{\lambda}(q^*, J_{\alpha}) dq^* \] \[ J_{\alpha} \text{ as function of } |\Psi^1|, |\Psi^2|, J_{\alpha} \in \text{運動積分} \]

直接選取 \( p_{\alpha} = \frac{\partial H}{\partial q^*} = \frac{\partial W}{\partial q^*} \)：

\[ \Rightarrow \dot{q}^* = \frac{\partial H}{\partial p_{\alpha}} = \frac{\partial}{\partial p_{\alpha}} W(q^*, J_{\alpha}) = \frac{\partial}{\partial J_{\alpha}} W(q^*, J_{\alpha}) \] \[ K = H + \frac{\partial W}{\partial t} = H \text{ in form of } \{ \omega^1, J^3 \} \] \[ K = H = E \in \text{運動積分} \] \[ 0 = \frac{d J_{\alpha}}{d t} = -\frac{\partial K}{\partial q^*} \Rightarrow K \text{ as function of } \{ J_{\alpha} \} \] \[ \dot{Q}^* = \frac{\partial K}{\partial p_{\alpha}} = \frac{\partial K(J_{\alpha})}{\partial J_{\alpha}} = \omega^1 (J_{\alpha}) \in \text{運動積分} \] \[ K = E - J_{\alpha} \in \text{運動積分} \] \[ \Rightarrow Q^*(t) = U^*(J_{\alpha}) t + Q^*(0) \]

後記
Index
Contact: