量子隨寫 Q Sketch
Author:Peir-Ru Wang
\(\to\)English Version
Update
(S33)2025.04.30: All-optical superconducting qubit readout
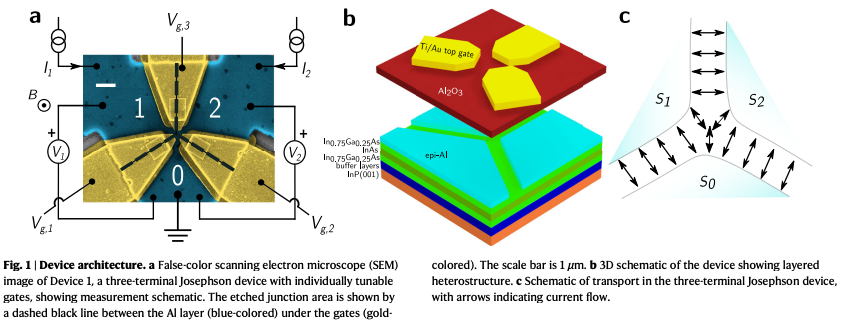
(S31)2025.04.29: Gate-tunable superconducting diode effect in a three-terminal Josephson device
(S29)2025.04.28: Wafer Scale \(MgB_2\)
(S27)2025.04.27: Sketch on Quantum Error, Error Correction, and Error Protection (II)
(S25)2025.04.26: Gatemon (Ge type)
(S23)2025.04.25: Gatemon
(S21)2025.04.24: Sketch on Quantum Error, Error Correction, and Error Protection (I)
(S19)2025.04.23: Prepare for Quantum Measurement: Interaction Basis
(S17)2025.04.18: About Flux-Pumped Josephson Parametric Amplifier (JPA)
(S16)2025.04.17: About Current-Pumped Josephson Parametric Amplifier (JPA)
(S15)2025.04.16: About Quantum Signal Amplify
(S14)2025.04.14: Transmon-Spin Hybrid Qubit
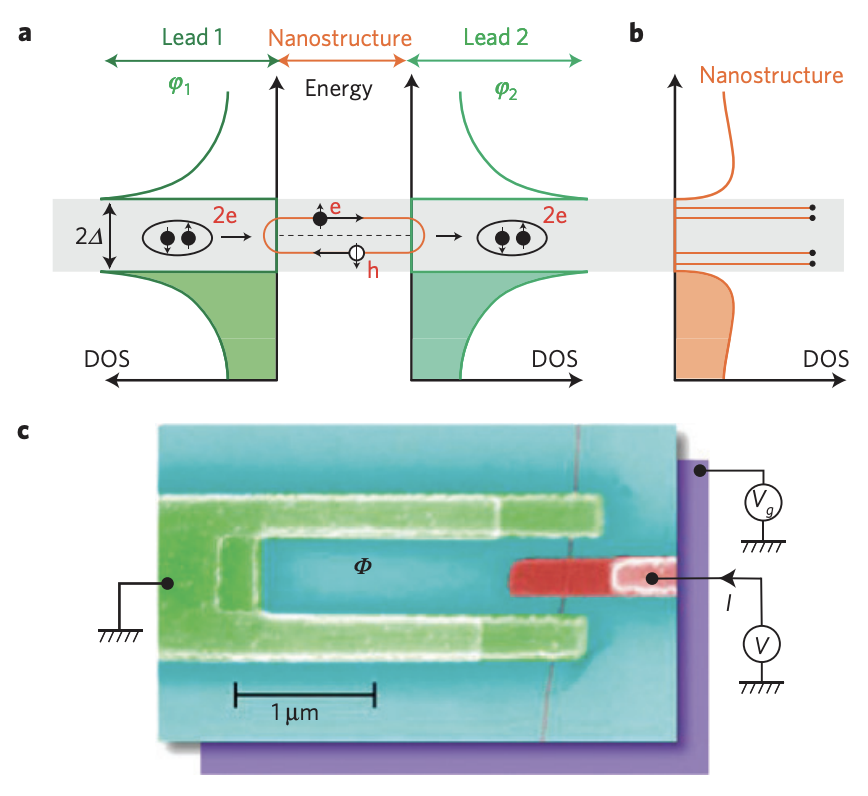
(S13)2025.04.13: Andreev Bound State (2010)
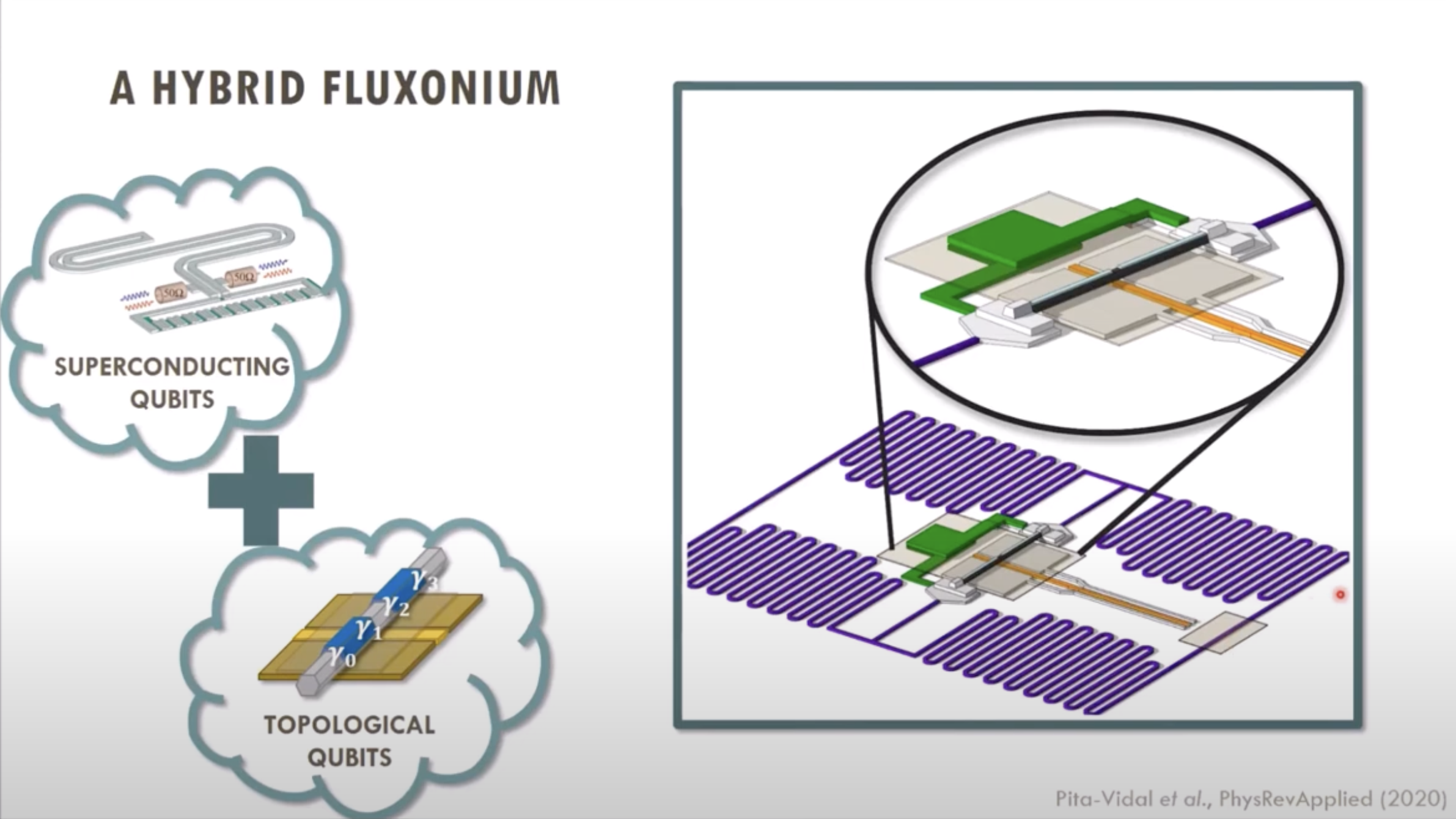
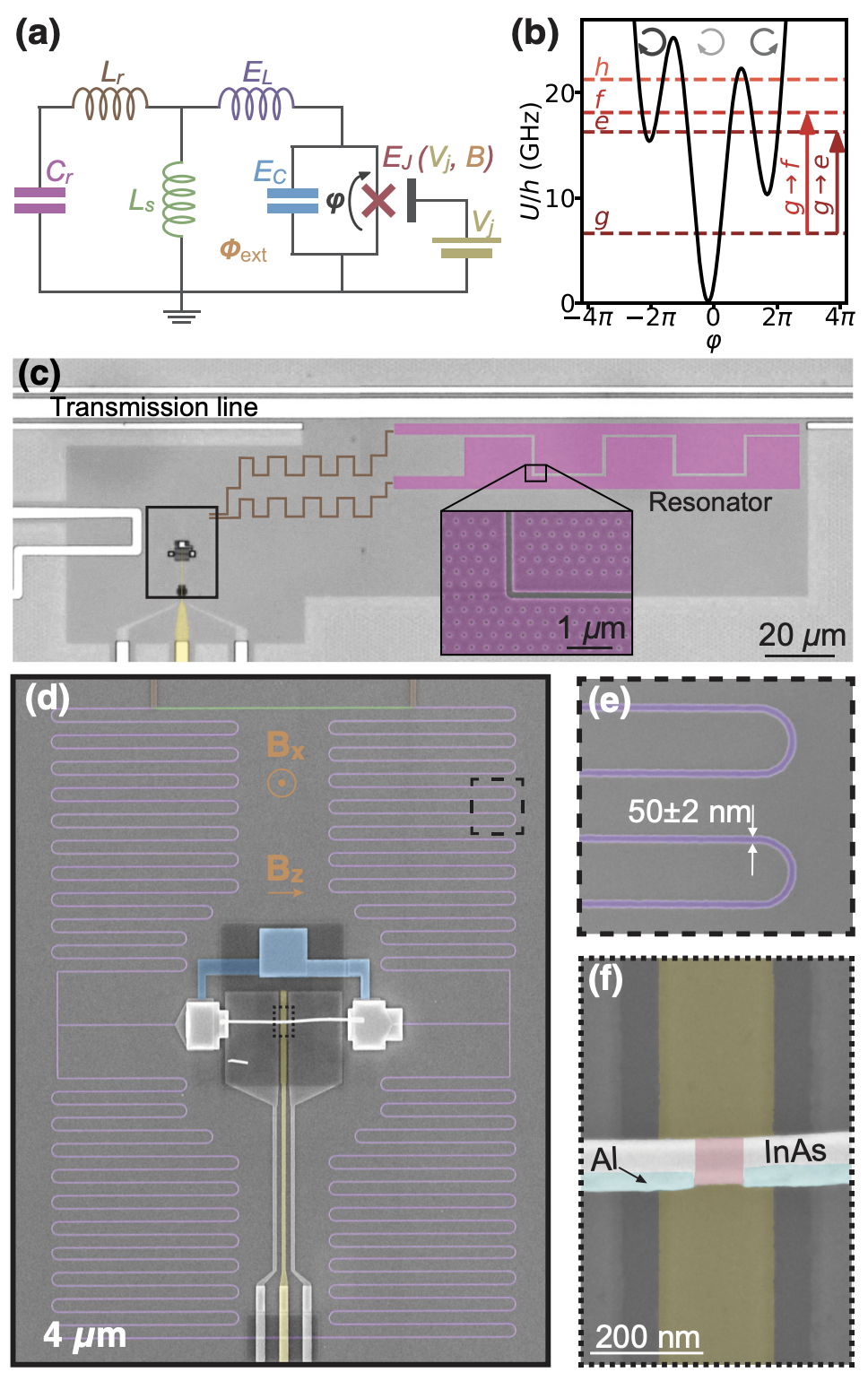
(S12)2025.04.12: Hybrid Type of Fluxonium (QuTech, 2021)
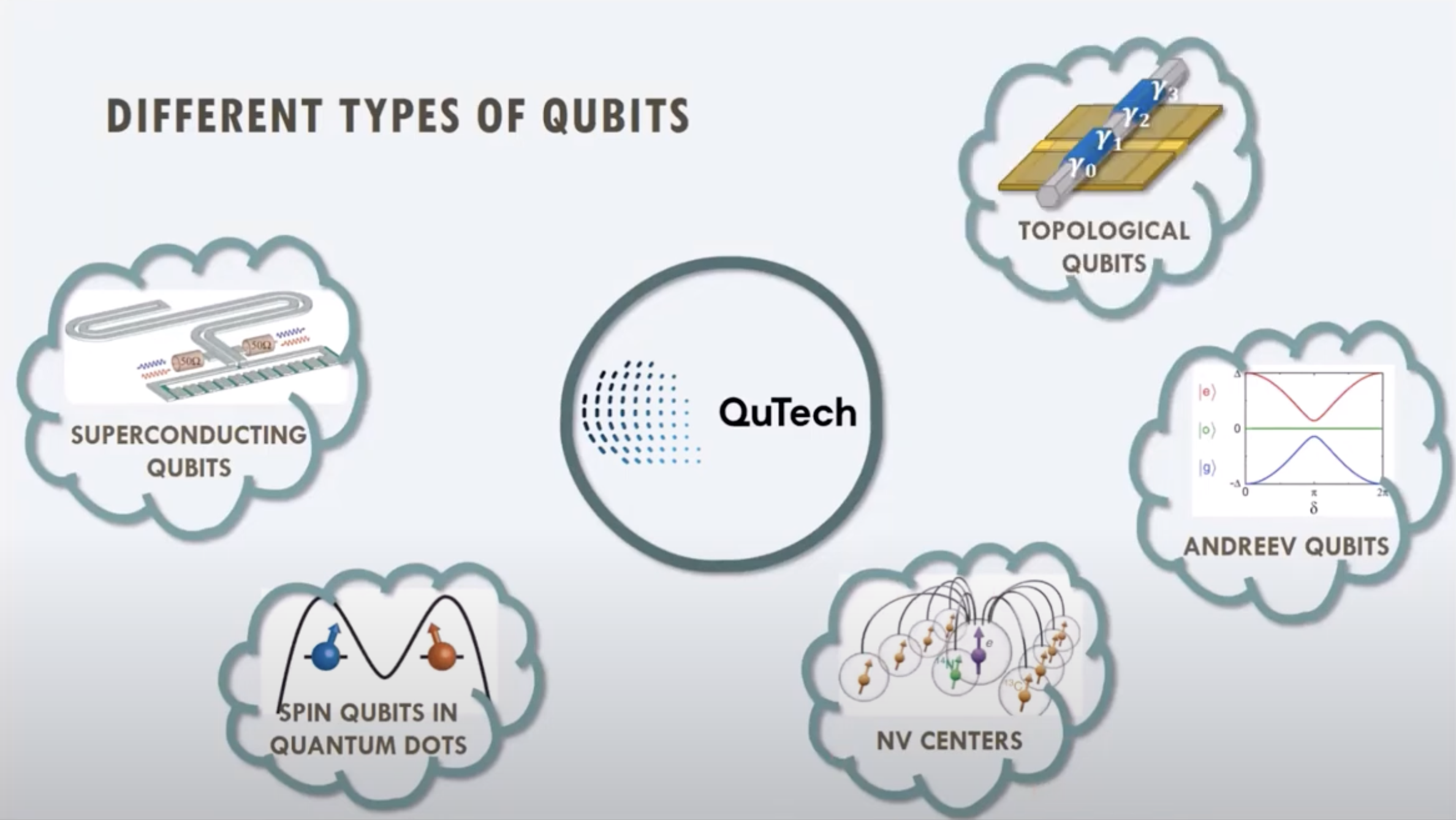
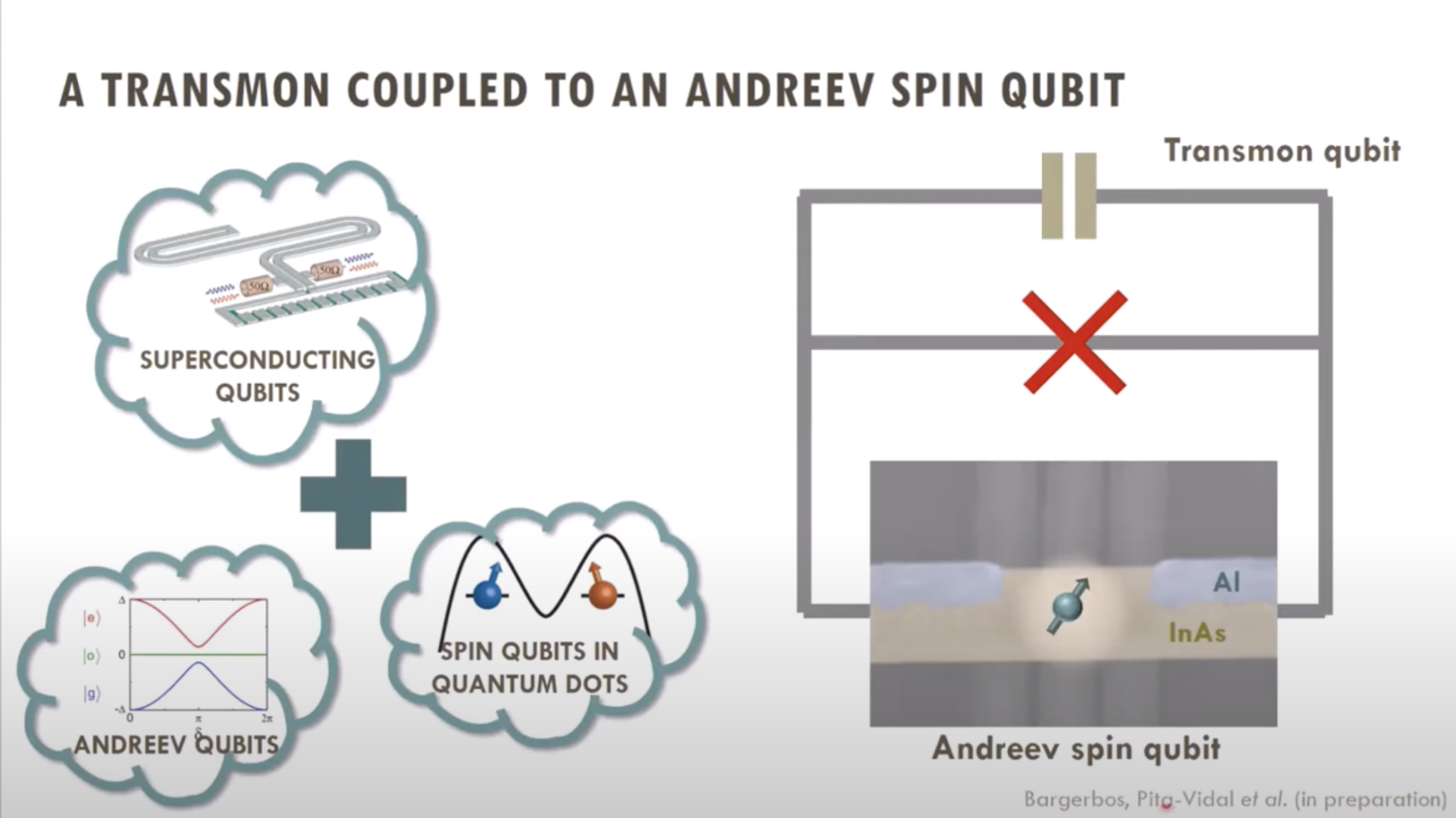
本篇為參考QuTech的演講\(^a\)。
演講中列舉五種QuTech在研究的量子位元:超導量子位元、自旋量子點量子位元、氮空缺鑽石量子位元(NV center)、Andreev量子位元、和拓墣量子位元。
有趣的是,除了氮空缺量子位元之外,自旋量子點量子位元、Andreev量子位元、和拓墣量子位元多少都與超導有關。
- 自旋量子點量子位元操作的溫度\( \leq 1K\),其操作的電極常進入超導狀態。可以參考\(\to\)後續文章。
- Andreev量子位元是利用Andreev反射製作的量子位元。可以參考\(\to\)後續文章。
- 拓墣量子位元常使用奈米線放置在超導體上,利用鄰近效應(Proximity Effect)使奈米線產生超導性,並在端點產生拓墣量子態。
Ref:
\(^a\)Youtube: "Hybrid Devices for Quantum Computing" by Marta Pita @ QuTech, TU Delft, https://www.youtube.com/watch?v=DWfjBdQMYCI
\(\to\)Gate-Tunable Field-Compatible Fluxonium, 2020, 10.1103/PhysRevApplied.14.064038
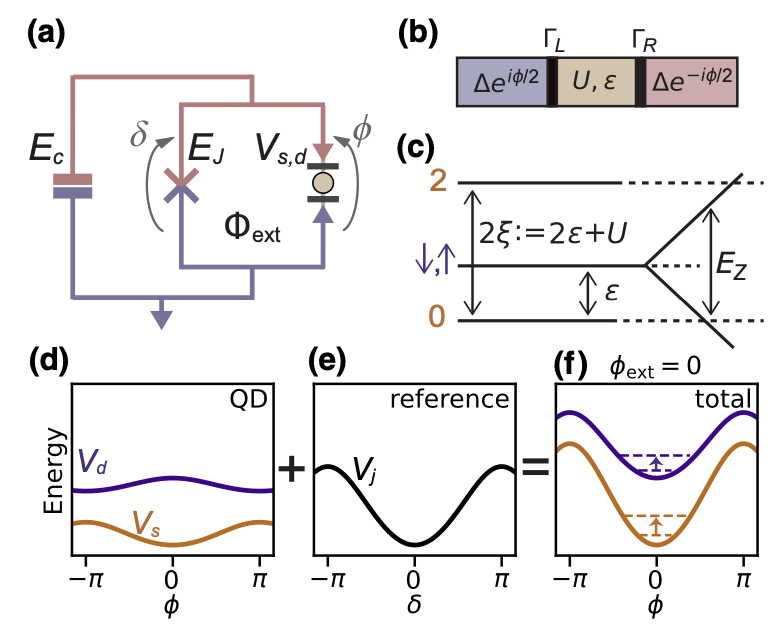
所謂Andreev反射是發生在非超導/超導接面中。因為超導體的原理是兩個電子形成的Cooper Pair,但是非導體中移動的載子是個別的單一電子,當單一電子從半導體穿隧進入到超導體時必須形成Cooper Pair,電荷守恆的要求下就會反射一個電洞。如果是超導/非超導/超導串接,中間的非超導區域會形成Andreev Bound State。
Ref:
\(\to\)"Andreev bound states in supercurrent-carrying carbon nanotubes revealed", 2010, DOI: 10.1038/nphys1811
Ref:
\(^a\)Youtube: "Hybrid Devices for Quantum Computing" by Marta Pita @ QuTech, TU Delft, https://www.youtube.com/watch?v=DWfjBdQMYCI
\(^b\) "Talks - Quantum Matter for Quantum Technologies 2024 - Marta PITA-VIDAL, IBM Zurich/TU Delft", https://www.youtube.com/watch?v=VEFzm_DcQ08
\(^c\) "Singlet-Doublet Transitions of a Quantum Dot Josephson Junction Detected in a Transmon Circuit", 2022, DOI: 10.1103/PRXQuantum.3.030311
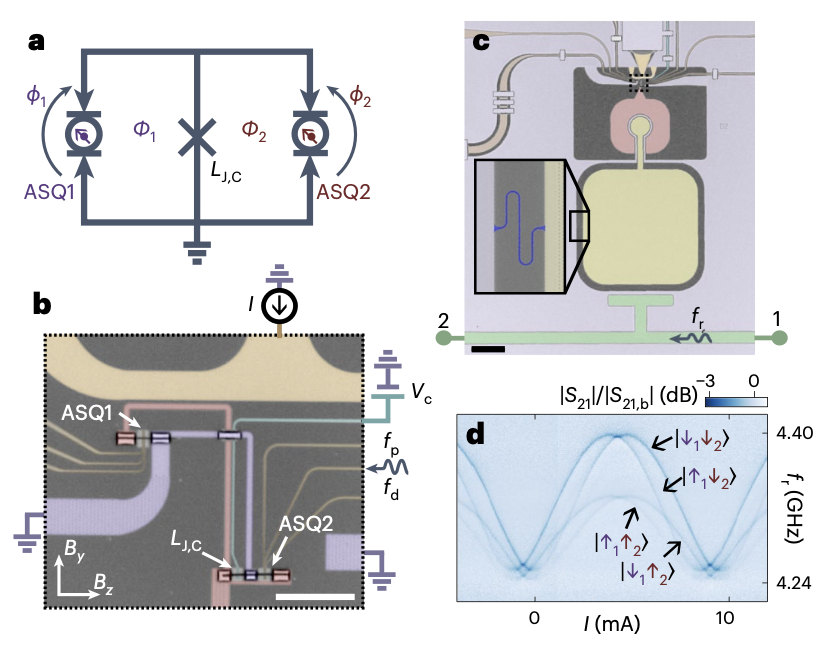
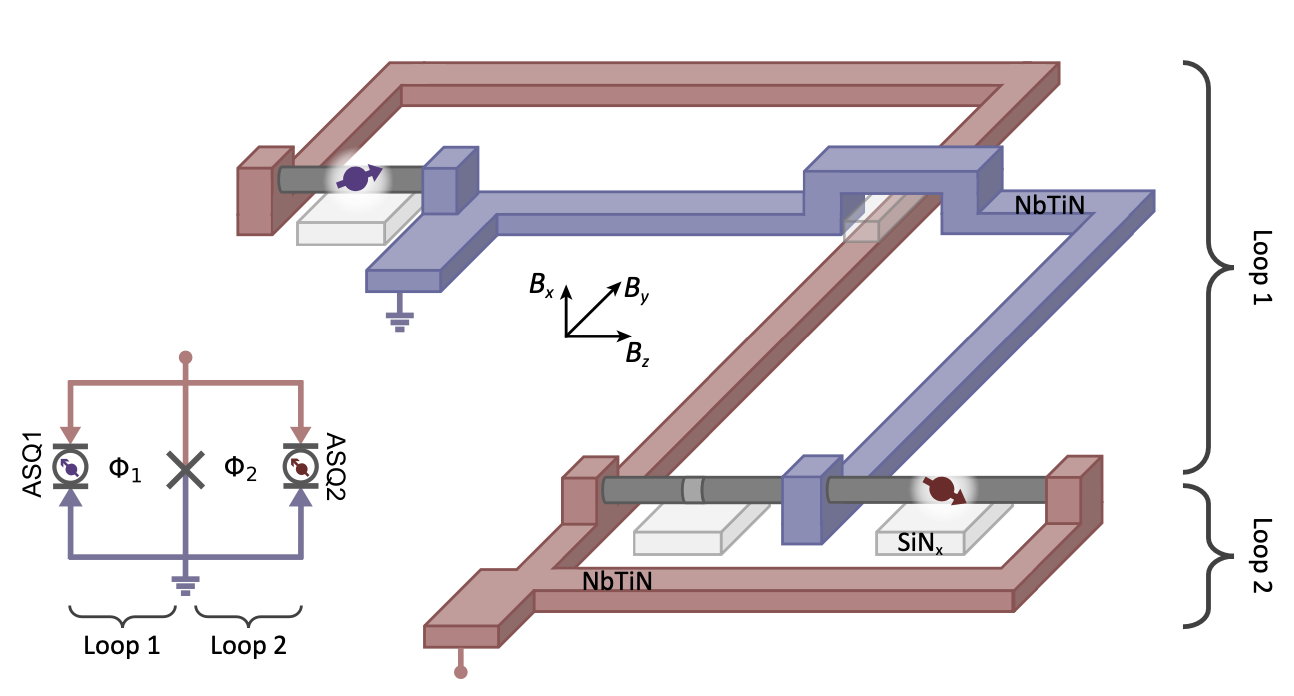
\(^d\) "Strong tunable coupling between two distant superconducting spin qubits", 2024, DOI: 10.1038/s41567-024-02497-x
本篇主要參考"A quantum engineer’s guide to superconducting qubits (2019)" \( ^a \)。
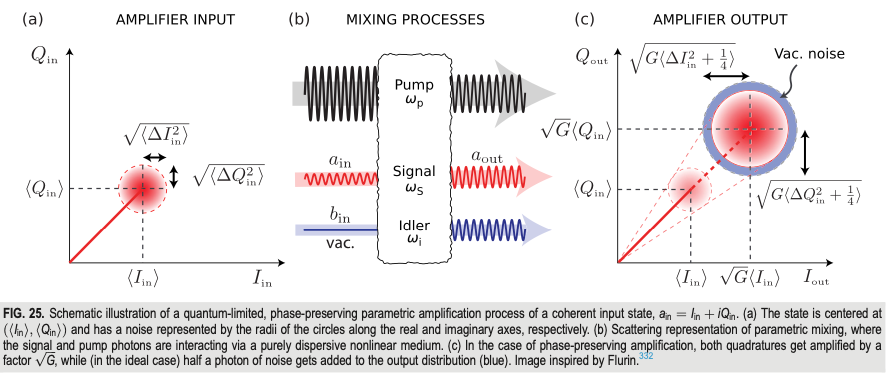
實現量子計算需要透過訊號去量測量子位元處在的量子態(Readout)。古典世界中量測手段基本上不影響被量測古典物理系統的狀態,換成物理的話來說就是量測的Hamiltonian遠小於系統的Hamiltonian。然而,量子世界裡量測訊號的數量級與系統常處在相同、甚至大於系統的能量級,故理解量測對於量子資訊是非常重要的議題。
要在超導量子電路中實踐有效的量子訊號放大,其中一種方式為利用約瑟夫森元件Josephson Junction製作而成的約瑟夫森參數放大器(Josephson Parametric Amplifier, JPA)。 根據能量守恆,想要放大訊號的能量,就需要輸入能量來提供額外的能量(Pump)。JPA常見的能量輸入有兩種,Current-Pumped(\(\to\) here)或是Flux-Pumped(\(\to\) here)。
Ref:
\( ^a \) "A quantum engineer’s guide to superconducting qubits (2019)", doi: 10.1063/1.5089550
延續前一篇提到量子訊號放大,本文參考\( ^{a,b} \)來介紹 Current-Pumped的JPA。
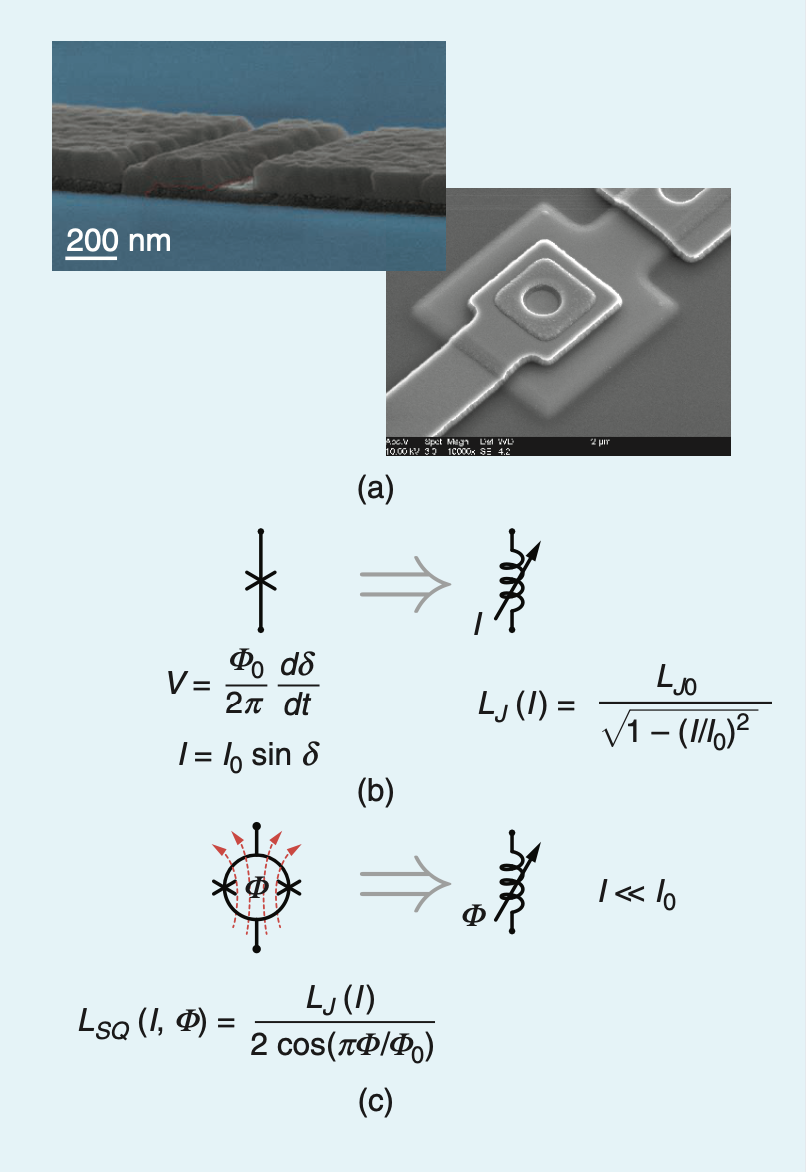
上圖(a)約瑟夫森節顯微鏡的圖(b)Current-Pumped JPA的物理原理(c)Flux-Pumped JPA的物理原理。本圖引用自\( ^{a} \)
利用約瑟夫的特性:(可以參考超導量子位元) \[ \frac{I\left( \Delta \psi \right)}{I_c}=sin \Delta \psi \] \[ L\left( \Delta \psi \right)=\frac{L_0}{cos \Delta \psi}\to L\left( I \right)= \frac{L_0}{\sqrt{1-\left( \frac{I\left( \Delta \psi \right)}{I_c}\right)^2}} \] 第一條式子可以想成施加電流\(I\)時,會對兩邊超導體形成\(\Delta \psi\)的相位差,帶入第二條可以理解為透過施加的電流可以控制電感大小\(L\)。 Current-Pumped JPA會施加頻率為\(\omega_p\)的交流電,作為能量來源。
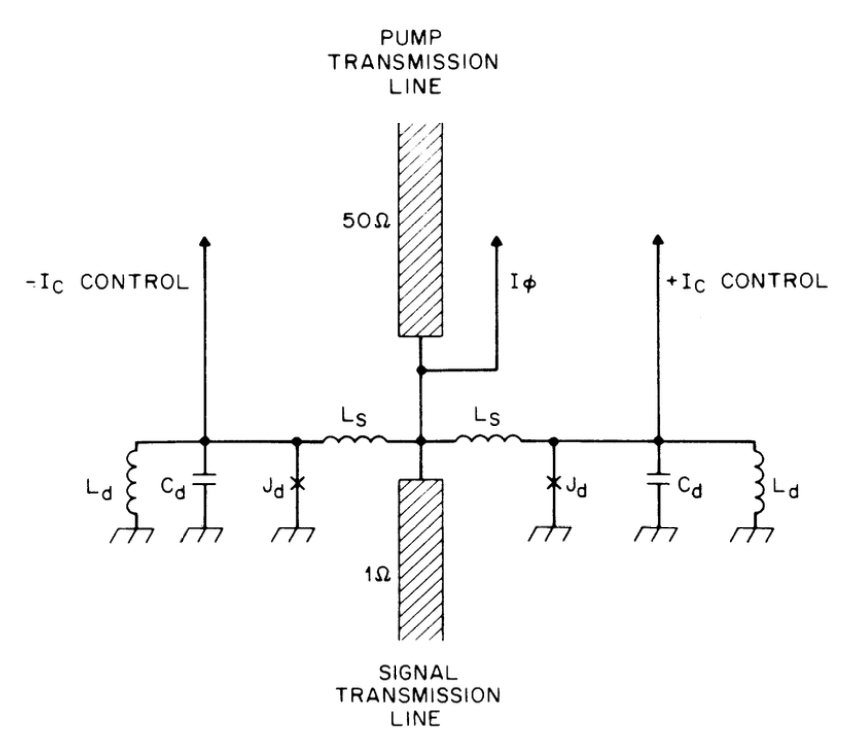
上圖為第一個實踐Current-Pumped JPA的論文介紹。引用自\( ^{b} \)
Ref:
\( ^a \) "Superconducting Parametric Amplifiers: The State of the Art in Josephson Parametric Amplifiers (2020)", Jose Aumentad, doi: 10.1109/MMM.2020.2993476
\( ^b \) "Observation of parametric amplification and deamplification in a Josephson parametric amplifier" (1989), 10.1103/PhysRevA.39.2519
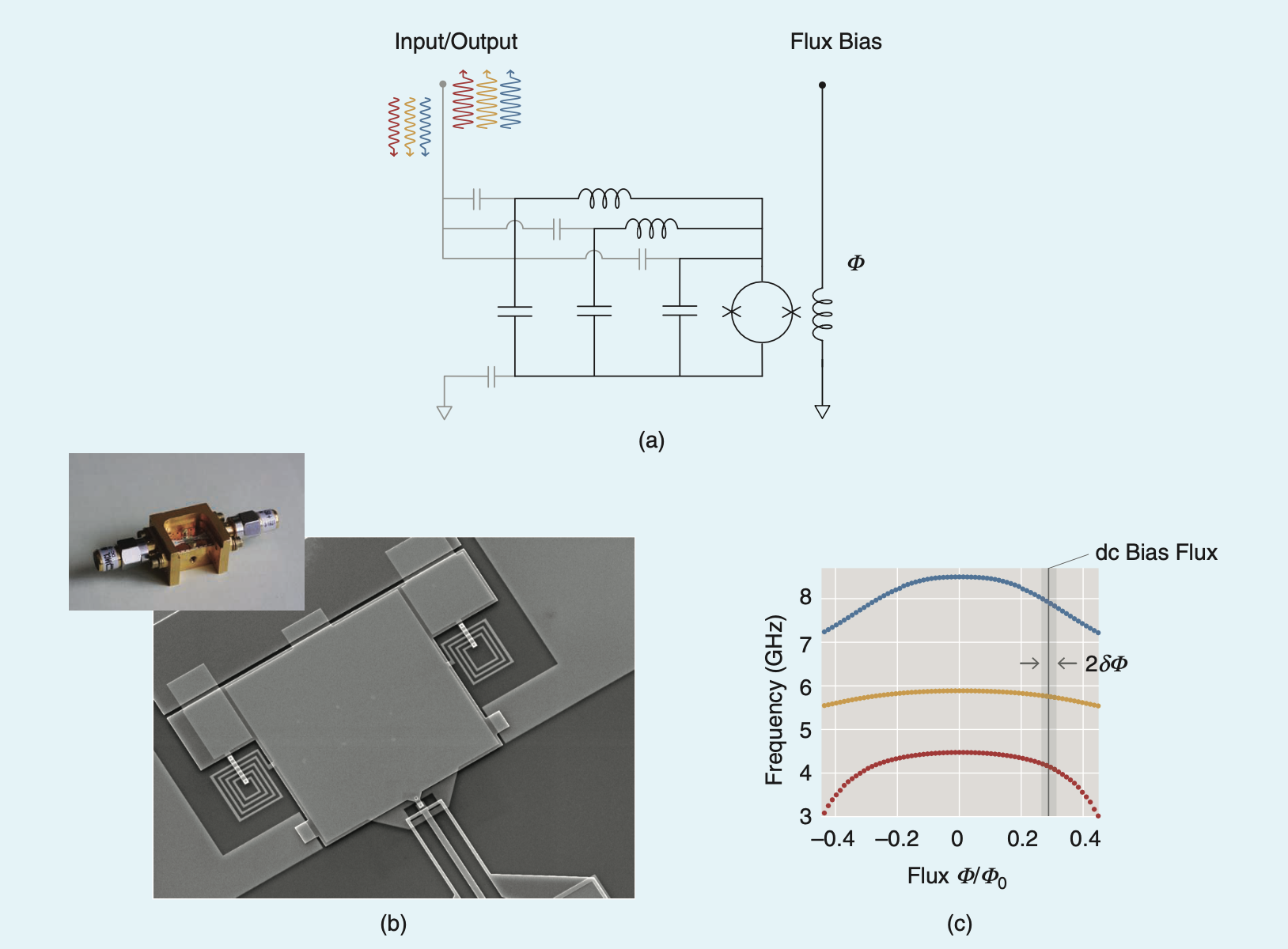
前一篇介紹Current-Pumped的JPA,本文一樣參考\( ^{a} \)來介紹 Flux-Pumped的JPA。
兩個約瑟夫森節並聯的電路稱作超導干涉元件(SQUID),此時因為量子電動力學的特性,量子波函數會與電磁規範場(Gauge Field)耦合,閉環的相位會與磁通量有關。 前文提及電感值\(L\)會與相位有關,故以SQUID製成的元件可以透過外部的Flux line來調控其電感特性。 此時我們可以透過Flux line 來施加頻率為\(\omega_p\)的變動磁通量,作為能量來源。
Ref:
\( ^a \) "Superconducting Parametric Amplifiers: The State of the Art in Josephson Parametric Amplifiers (2020)", Jose Aumentad, doi: 10.1109/MMM.2020.2993476
The interaction basis is the same as the interaction picture in standard textbooks.
\[ i\hbar \partial_t |\psi_0(t)\rangle = H_0(t) |\psi_0(t)\rangle \] \[ |\psi_0(t)\rangle = e^{-\frac{i}{\hbar} \mathcal{T}\left[\int_0^t H_0(\mathscr{t})\,d\mathscr{t} \right]} |\psi_0(0)\rangle \equiv U_0(t)|\psi_0(0)\rangle \]
\[ i \partial_t U_0(t) = H_0(t) U_0(t) \] \[ -i \partial_t U_0^\dagger(t) = U_0^\dagger(t) H_0(t) \]
\[ i\hbar \partial_t |\psi(t)\rangle = [H_0(t) + H_I(t)] |\psi(t)\rangle \] \[ |\Theta(t)\rangle \equiv U_0^\dagger(t) |\psi(t)\rangle \]
\[ \begin{aligned} i\hbar \partial_t |\Theta(t)\rangle &= i \partial_t [U_0^\dagger(t) |\psi(t)\rangle] \\ &= i\hbar \partial_t U_0^\dagger(t) * |\psi(t)\rangle + U_0^\dagger(t) * i\hbar \partial_t |\psi(t)\rangle \\ &= -U_0^\dagger(t) H_0(t) * |\psi(t)\rangle + U_0^\dagger(t)[H_0(t) + H_I(t)] |\psi(t)\rangle \\ &= U_0^\dagger(t) H_I(t) |\psi(t)\rangle = U_0^\dagger(t) H_I(t) U_0(t) U_0^\dagger(t) |\psi(t)\rangle \\ &= U_0^\dagger(t) H_I(t) U_0(t) |\Theta(t)\rangle \end{aligned} \]
\[ i\hbar \partial_t |\Theta(t)\rangle = U_0^\dagger(t) H_I(t) U_0(t) |\Theta(t)\rangle \]
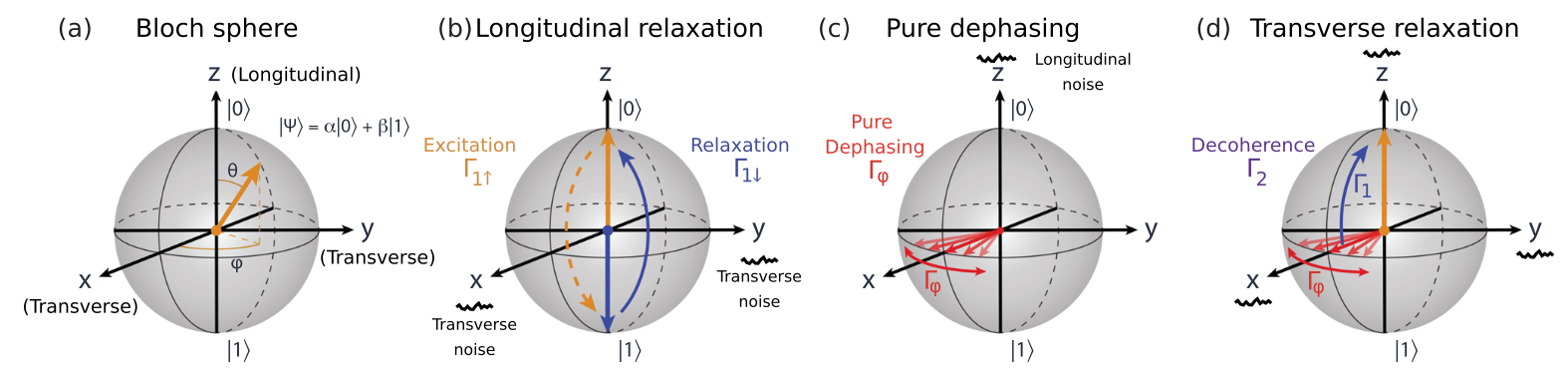
量子計算目前遇到很大的瓶頸是高錯誤率,如果以Gate base量子電腦來說,最簡單錯誤分法可以分成單量子位元錯誤(Single qubit error)和閘控錯誤(Gate error)。 這篇先以單量子位元錯誤為討論基礎。
單量子位元錯誤可以從能量的觀點來看,一個量子態的演化遵守薛丁格方程式: \[ i\hbar \partial_t \ket{\psi\left(t\right)}=\hat{H}\left(t\right) \ket{\psi\left(t\right)} \leftrightarrow \ket{\psi\left(t\right)}=e^{-\frac{i}{\hbar}\mathcal{T}\left[\int^t_0\hat{H}\left(\mathscr{t}\right)d\mathscr{t}\right]}\ket{\psi\left(0\right)} \] 這邊\( \mathcal{T}\left[\int^t_0\hat{H}\left(\mathscr{t}\right)d\mathscr{t} \right]\)是time order積分,因為不同時刻的Hamiltonian不一定commute, \[ \left[\hat{H}\left(t_1\right),\hat{H}\left(t_2\right)\right]\neq 0 \] 是量子系統演化比較複雜的部分。如果剛好滿足對易的話,則積分就會回復到常見的形式 \[ \mathcal{T}\left[\int^t_0\hat{H}\left(\mathscr{t}\right)d\mathscr{t}\right]_{\left[\hat{H}\left(t_1\right),\hat{H}\left(t_2\right)\right]= 0} =\hat{H} * t \leftrightarrow \ket{\psi\left(t\right)}=e^{-\frac{it}{\hbar}\hat{H}}\ket{\psi\left(0\right)} \]Ref. Gatemons get serious, Nature Nanotechnology (2018), Doi:10.1038/s41565-018-0218-8
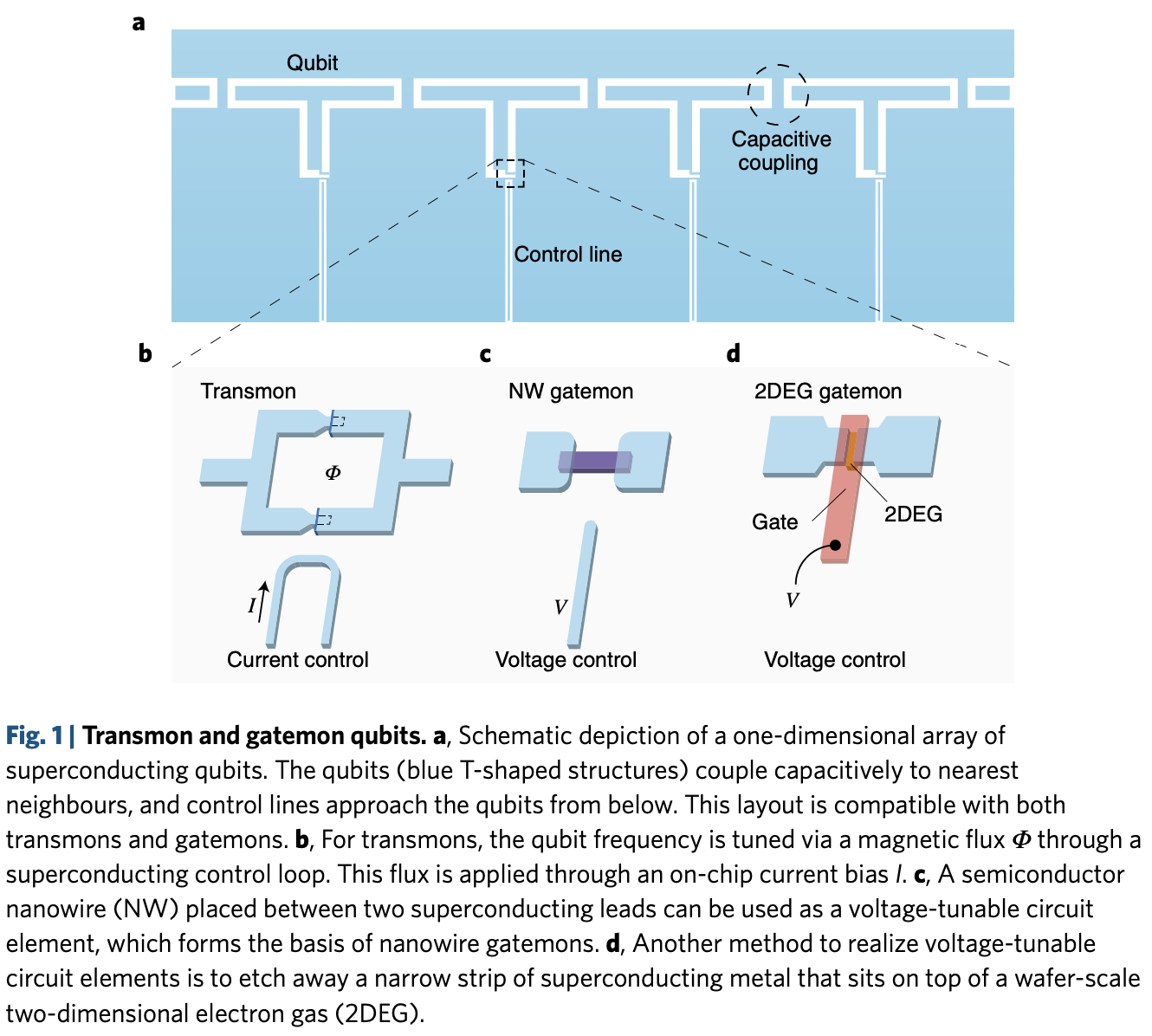
Gatemon也是一種以超導材料為基礎的量子位元,結合類似Gate-define spin qubit的架構。在約瑟夫森節的部分導入閘控電壓,來控制量子位元的特性。 上圖中(b.)在Tunable Transmon中,利用flux line通入磁通量來調整SQUID的等效電感,藉此來調整transomon的頻率。 (c,d)則是兩種不同實踐Gatemon的方式。
Ref. Superconducting gatemon qubit based on a proximitized two-dimensional electron gas, Nature Nanotechnology (2018), Doi:10.1038/s41565-018-0207-y
上圖中以\(Al\)基約瑟夫森節,去調控\(InAs\)的2DEG(二維電子氣,2D electron gas)。
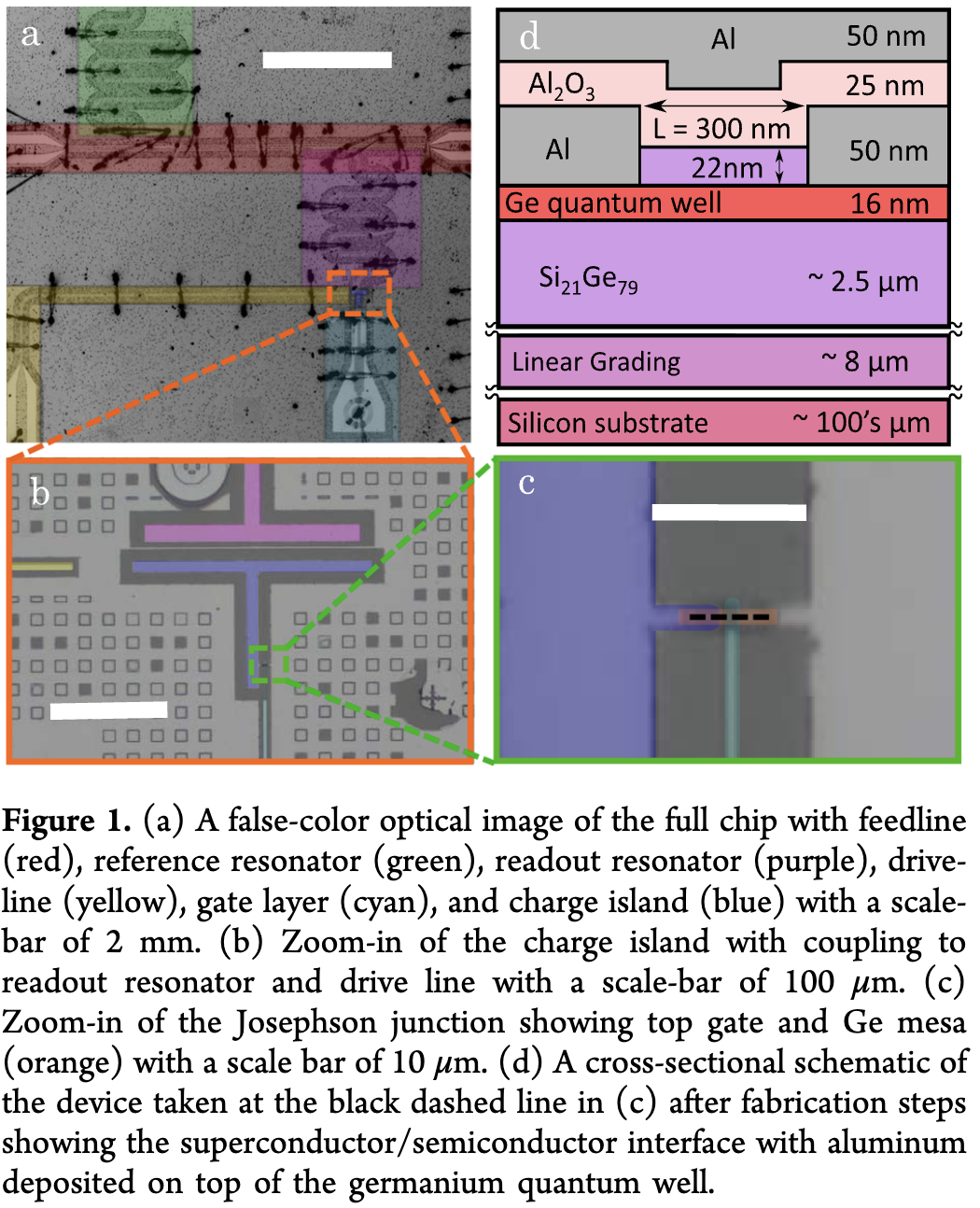
Ref. Gatemon Qubit on a Germanium Quantum-Well Heterostructure, Nano Letter (2024), Doi:10.1021/acs.nanolett.4c05539
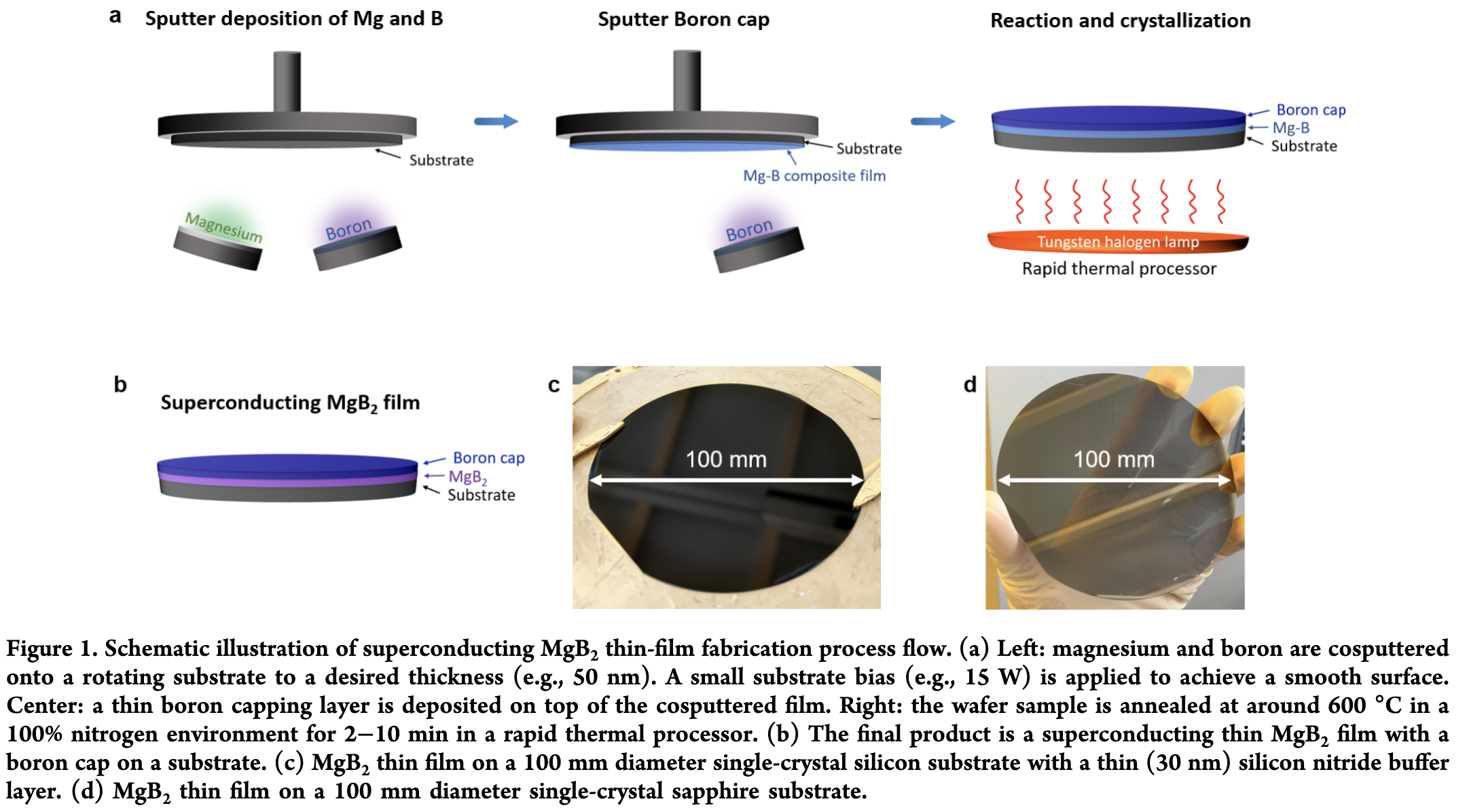
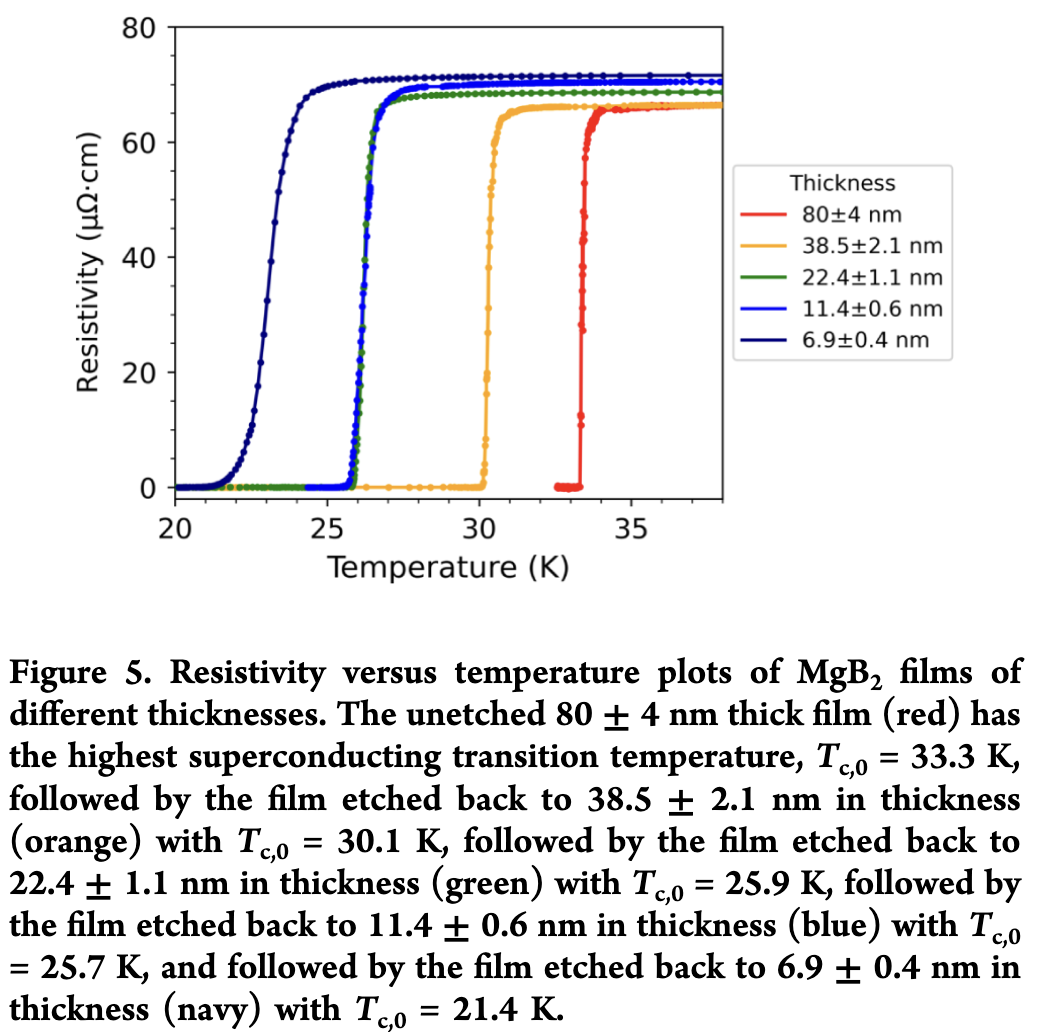
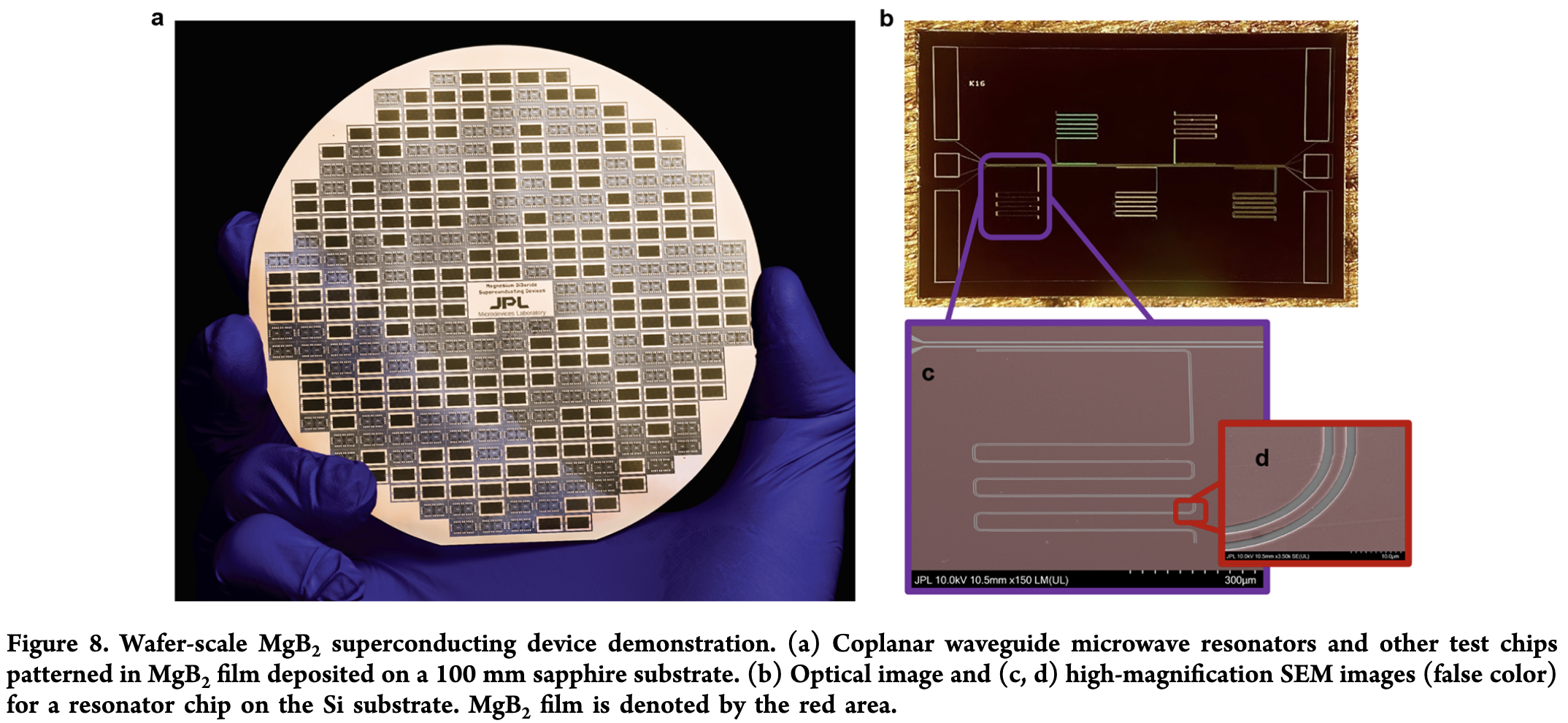
\(MgB_2\)作為目前傳統超導體(可由BCS理論解釋的超導)最高的臨界溫度\(T_c =40K\),有機會作為較高溫度的量子位元應用。 目前常用的超導量子位元材料\(Al, T_c^{Al}=1.2K\)、\(Nb, T_c^{Nb}=9.2K\),常操作在\(10mK\)低溫下,需要極大的冷卻功率。 當前常說的“Hot Qubit”,實際上是能在\(1K\)穩定操作的量子位元,就已經可以大幅降低冷卻系統的功率。 以薄膜製程而言,當元素不只一種時,就容易有元素比例變動的問題需要解決。 故研制出大尺寸的\(MgB_2\)也是一個技術上重要的進展。
改變超導臨界溫度一直是我非常有興趣的題目,我博士期間的研究就是試圖尋找一個框架來理解如何改變臨界溫度,可以參考這裡。 \(MgB_2\)的臨界溫度亦可以透過薄膜厚度來調整。
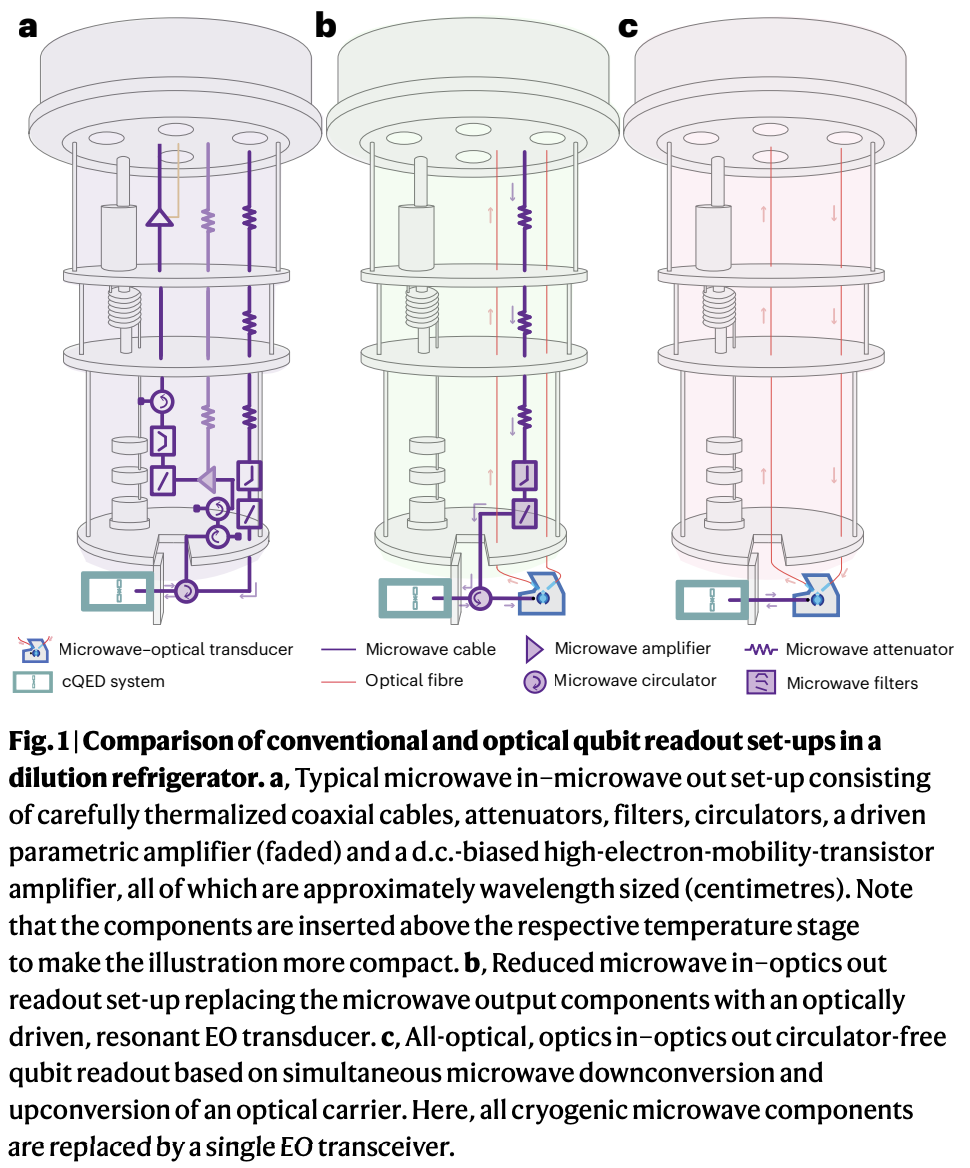
目前超導量子位元的控制依賴微波電信號,然而通往數千超導量子位元的控制,就需要超過千條以上的信號線,從外界室溫穿越低溫桶,進入到\(10mK\)的位元硬體區域。 然而如此多的線路,佈線極其複雜,而且也會從外界引入熱量及熱噪音,造成硬體失效、需要更大的製冷功率。 故目前一直尋找全光控制,試圖利用光纖來替代微波電路。
後記
Index
Contact:
![]()